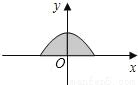
如图所示是二次函数y=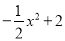
的图象在x轴上方的一部分，对于这段图象与x轴所围成的阴影部分的面积，你认为可能的值是（ ）
A. 4 B.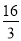 
C. 2π D. 8
B
【解析】函数与y轴交于（0，2）点，与x轴交于（-2，0）和（2，0）两点，则三点构成的三角形面积S1=4，则以半径为2的半圆的面积为S2=π××22=2π，则阴影部分的面积S有：4＜S＜2π．因为选项A、C、D均不在S取值范围内．故选 B 周长8m的铝合金制成如图所示形状的矩形窗柜，使窗户的透光面积最大，那么这个窗户的最大透光面积是（）m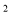
A.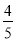 
B.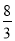 
C. 4 D.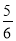 
B
【解析】设窗户的宽是x，根据题意得
S=
=
∴当窗户宽是m时，面积最大是m²,故选B. 如图，从地面竖直向上抛出一个小球，小球的高度h（单位：m）与小球运动时间t（单位：s）之间的关系式为h=30t-5t2，那么小球从抛出至回落到地面所需要的时间是（ ）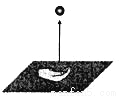
A. 6s B. 4s C. 3s D. 2s
A
【解析】试题分析：由小球高度h与运动时间t的关系式h=30t﹣5t2，令h=0，解得的两值之差便是所要求得的结果．
由小球高度h与运动时间t的关系式h=30t﹣5t2． 令h=0，﹣5t2+30t=0 解得：t1=0，t2=6
△t=6，小球从抛出至回落到地面所需要的时间是6秒． 如图，二次函数y= -x2-2x的图象与x轴交于点A、O，在抛物线上有一点P，满足
S△AOP=3，则点P的坐标是（ ）
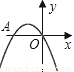
A. （-3，-3） B. （1，-3） C. （-3，-3）或（-3，1） D. （-3，-3）或（1，-3）
D
【解析】分析：根据抛物线的解析式，即可确定点A的坐标，由于OA是定长，根据△AOP的面积即可确定P点纵坐标的绝对值，将其代入抛物线的解析式中，即可求得P点的坐标．
解答：【解析】
抛物线的解析式中，令y=0，得：-x2-2x=0，解得x=0，x=-2；
∴A（-2，0），OA=2；
∵S△AOP=OA?|yP|=3，∴|yP|=3；
当P点纵坐标为3时，-x2-... 向空中发射一枚炮弹，经x秒后的高度为y米，且时间与高度的关系为y=ax2bx+c（a≠0）．若此炮弹在第7秒与第14秒时的高度相等，则在下列时间中炮弹所在高度最高的是（ ）
A. 第8秒 B. 第10秒 C. 第12秒 D. 第15秒
B
【解析】试题分析：炮弹在第7秒与第14秒时的高度相等所以抛物线的对称轴是在第10秒处，所以在第10秒处高度是最高的.
故选B. 将进货单价为70元的某种商品按零售价100元一个售出时，每天能卖出20个，若这种商品的零售价每降价1元，其日销量就增加1个，为了获取每日最大利润，则应降价（ ）
A. 5元 B. 10元 C. 15元 D. 20元
A
【解析】设应降价x元，总利润为y元，根据题意可得：
，
化简、配方得：
，
∴当时，y最大=625，
∴ B、C、D错误，选A. 如图，正方形ABCD的边长为1，E、F分别是边BC和CD上的动点（不与正方形的顶点重合），不管E、F怎样动，始终保持AE⊥EF．设BE=x，DF=y，则y是x的函数，函数关系式是（ ）
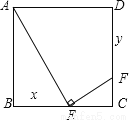
A. y=x+1 B. y=x-1 C. y=x2-x+1 D. y=x2-x-1
C
【解析】试题分析：易证△ABE∽△ECF，根据相似三角形对应边的比相等即可求解．
【解析】
∵∠BAE和∠EFC都是∠AEB的余角．
∴∠BAE=∠FEC．
∴△ABE∽△ECF
那么AB：EC=BE：CF，
∵AB=1，BE=x，EC=1﹣x，CF=1﹣y．
∴AB•CF=EC•BE，
即1×（1﹣y）=（1﹣x）x．
化简得：y=x2... 如图所示，桥拱是抛物线形，其函数的表达式为y= -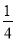
x2，当水位线在AB位置时，水面宽12m，这时水面离桥顶的高度为（ ）
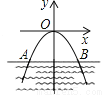
A. 3m B.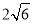 
m C.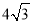 
m D. 9 m
D
【解析】试题解析：由已知知：
点的横坐标为.
把代入
得
即水面离桥顶的高度为
故选D. 如图，隧道的截面是抛物线，可以用y=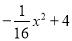 
表示，该隧道内设双行道，限高为3m，那么每条行道宽是（ ）
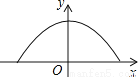
A. 不大于4m B. 恰好4m C. 不小于4m D. 大于4m，小于8m
A
【解析】把y=3代入y= 中得：
x=4，x= -4（舍去）．
∴每条行道宽应不大于4m．
故选A．
点睛；本题考查二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．由题意可知，直接把y=3代入解析式求解即可． 如图，一边靠校园围墙，其他三边用总长为40米的铁栏杆围成一个矩形花圃，设矩形ABCD的边AB为x米，面积为S平方米，要使矩形ABCD面积最大，则x的长为（ ）
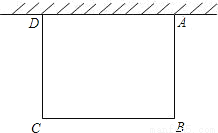
A. 10米 B. 15米 C. 20米 D. 25米
A
【解析】设矩形ABCD的边AB为x米，则宽为40-2x，
S=（40-2x）x= -2x2+40x．
要使矩形ABCD面积最大，
则
即x的长为10m．
故选A．