如图，某校的围墙由一段相同的凹曲拱组成，其拱状图形为抛物线的一部分，栅栏的跨径AB间，按相同间隔0.2米用5根立柱加固，拱高OC为0.36米，则立柱EF的长为（ ）
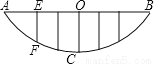
A. 0.4米 B. 0.16米 C. 0.2米 D. 0.24米
C
【解析】如图，以C坐标系的原点，OC所在直线为y轴建立坐标系，
设抛物线解析式为y=ax2，由题知，图象过B（0.6，0.36），代入得：0.36=0.36a
∴a=1，即y=x2．∵F点横坐标为-0.4，∴当x=-0.4时，y=0.16，∴EF=0.36-0.16=0.2米.故选C． 小敏在某次投篮中，球的运动路线是抛物线y=﹣
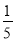x2+3.5的一部分（如图），若命中篮圈中心，则他与篮底的距离L是（ ）
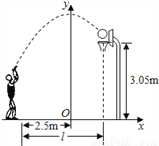
A. 3.5m B. 4m C. 4.5m D. 4.6m
B
【解析】试题分析：如图，把C点纵坐标y=3.05代入y=x2+3.5中得： x=±1.5（舍去负值），
即OB=1.5， 所以L=AB=2.5+1.5=4米，故选B． 如图，已知⊙P的半径为2，圆心P在抛物线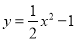
上运动，当⊙P与x轴相切时，圆心P的坐标为_____________
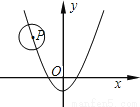
（，2）或（，2）
【解析】试题分析：依题意，可设P（x，2）或P（x，﹣2）．
①当P的坐标是（x，2）时，将其代入y=x2﹣1，得
2=x2﹣1，
解得x=±，
此时P（，2）或（﹣，2）；
②当P的坐标是（x，﹣2）时，将其代入y=x2﹣1，得
﹣2=x2﹣1，即﹣1=x2
无解．
综上所述，符合条件的点P的坐标是（，2）或（﹣，2） 如图，在相距2米的两棵树间拴一根绳子做一个简易的秋千.拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小芳距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为 米.
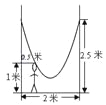
0.5
【解析】试题分析：首先以点名所在的直线为x轴，最低点所在的直线为y轴建立平面直角坐标系，然后求出二次函数的解析式，最后计算出顶点坐标，顶点坐标的纵坐标就是距离地面的距离. 如图，已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米，AC与MN在同一直线上，开始时点A与点N重合，让△ABC以每秒2厘米的速度向左运动，最终点A与点M重合，则重叠部分面积y（厘米2）与时间t（秒）之间的函数关系式为____
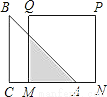
y=（20-2t）2
【解析】AM=20-2t，则重叠部分面积y=×AM2= （20-2t）2 如图，点A1、A2、A3、…、An在抛物线y=x2图象上，点B1、B2、B3、…、Bn在y轴上，若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形（点B0是坐标原点），则△A2015B2014B2015的腰长=____
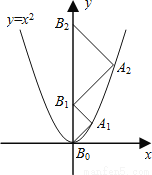
2015
【解析】作A1C⊥y轴，A2E⊥y轴，垂足分别为C、E．
∵△A1BOB1、△A2B1B2都是等腰直角三角形
∴B1C=B0C=DB0=A1D，B2E=B1E=A2E
∴设A1（a，a）将其代入解析式y=x2得：
∴a=a2
解得：a=0（不符合题意）或a=1，由勾股定理得：A1B0=
同理可以求得：A2B1=2
A3B2=3
A4B... 如图，在△ABC中，∠B=90°，AB=12mm，BC=24mm，动点P从点A开始沿边AB向B以2mm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向C以4mm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，那么经过 秒，四边形APQC的面积最小．
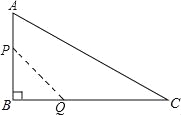
3
【解析】
试题分析：根据等量关系“四边形APQC的面积=三角形ABC的面积﹣三角形PBQ的面积”列出函数关系
最小值． 设P、Q同时出发后经过的时间为ts，四边形APQC的面积为Smm2，
则有：S=S△ABC﹣S△PBQ==4t2﹣24t+144=4（t﹣3）2+108．
∵4＞0 ∴当t=3s时，S取得最小值． 扎西的爷爷用一段长30m的篱笆围成一个一边靠墙的矩形菜园，墙长为18m，这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？
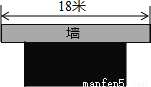
当矩形的长为15m，宽为7.5m时，矩形菜园的面积最大，最大面积为112.5m2
【解析】试题分析：设菜园宽为x，则长为36-2x，由面积公式写出y与x的函数关系式，然后利用二次函数的最值的知识可得出菜园的最大面积，及取得最大面积时矩形的长和宽．
设长为x米，宽为(30-x)/2米-,面积为y米2
当x=15时，y最大=112.5
答：最大面积是112.5米2． 某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y= -2x+100．（利润=售价-制造成本）
（1）写出每月的利润z（万元）与销售单价x（元）之间的函数关系式；
（2）当销售单价为多少元时，厂商每月能获得350万元的利润？当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？
（1）z= -2x2+136x-1800；（2）当销售单价为34元时，每月能获得最大利润，最大利润是512万元；
【解析】试题分析：（1）根据每月的利润z=（x-18）y，再把y=-2x+100代入即可求出z与x之间的函数解析式，
（2）把z=350代入z=-2x2+136x-1800，解这个方程即可，将z═-2x2+136x-1800配方，得z=-2（x-34）2+512，即可求出当... 每年六七月份我市荔枝大量上市，今年某水果商以5元/千克的价格购进一批荔枝进行销售，运输过程中质量损耗5%，运输费用是0.7元/千克，假设不计其他费用．
（1）水果商要把荔枝售价至少定为多少才不会亏本？
（2）在销售过程中，水果商发现每天荔枝的销售量m（千克）与销售单价x（元/千克）之间满足关系：m= -10x+120，那么当销售单价定为多少时，每天获得的利润w最大？
（1）水果商要把荔枝售价至少定为6元/千克才不会亏本（2）当销售单价定为9元/千克时，每天可获利润w最大
【解析】分析：（1）设购进荔枝a千克，荔枝售价定为b元/千克时，水果商要不亏本，由题意建立不等式求出其值就可以了．
（2）由（1）可知，每千克荔枝的平均成本为6元，再根据售价-进价=利润就可以表示出w，然后化为顶点式就可以求出最值．
本题解析：
（1）设购进荔枝a千克，...