题目内容
如图，某校的围墙由一段相同的凹曲拱组成，其拱状图形为抛物线的一部分，栅栏的跨径AB间，按相同间隔0.2米用5根立柱加固，拱高OC为0.36米，则立柱EF的长为（ ）
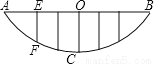
A. 0.4米 B. 0.16米 C. 0.2米 D. 0.24米
C
【解析】如图，以C坐标系的原点，OC所在直线为y轴建立坐标系，
设抛物线解析式为y=ax2，由题知，图象过B（0.6，0.36），代入得：0.36=0.36a
∴a=1，即y=x2．∵F点横坐标为-0.4，∴当x=-0.4时，y=0.16，∴EF=0.36-0.16=0.2米.故选C．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案下列多项式中能用平方差公式分解因式的是（ ）
A．a2+（﹣b）2 B．5m2﹣20mn C．﹣x2﹣y2 D．﹣x2+9
D．
【解析】
试题分析：A、a2+（﹣b）2符号相同，不能用平方差公式分解因式，故A选项错误；
B、5m2﹣20mn两项不都是平方项，不能用平方差公式分解因式，故B选项错误；
C、﹣x2﹣y2符号相同，不能用平方差公式分解因式，故C选项错误；
D、﹣x2+9=﹣x2+32，两项符号相反，能用平方差公式分解因式，故D选项正确．
故选D． 气象台发布的卫星云图显示,代号为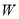
的台风在某海岛(设为点
)的南偏东
方向的
点生成,测得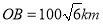
.台风中心从点
以
的速度向正北方向移动，经
后到达海面上的点
处.因受气旋影响,台风中心从点
开始以
的速度向北偏西
方向继续移动.以
为原点建立如图所示的直角坐标系．
(1)台风中心生成点
的坐标为 ,台风中心转折点
的坐标为 ；(结果保留根号)
(2)已知距台风中心
范围内均会受到台风侵袭.如果某城市(设为点
)位于点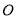
的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间？
（1）（2）台风从生成到最初侵袭该城要经过小时
【解析】试题分析：(1)、根据直角三角形中特殊角的三角函数值分别求出点B和点C的坐标；(2)、过点C作CD⊥OA于点D，则∠ACD=30°，根据Rt△ACD中∠ACD的余弦值得出AC的长度，从而求出时间得出答案．
试题解析：(1) :
(2)过点作于点,则,
在Rt中, ，
∴，
∵， ，
∴台风从生成到最初... 如图，从热气球C处测得地面A、B两点的俯角分别是30°、45°.如果此时热气球C处的高度CD为100米，点A、D、B在同一直线上，则AB两点的距离是( )
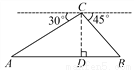
A. 200米 B. 200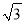
米 C. 220
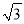米 D. 100(
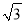＋1)米
D
【解析】试题分析：根据平行线的性质可得：∠A=30°，∠B=45°．在Rt△ACD中，tan∠A=tan30°=，则AD=米；在Rt△CDB中，tan∠B=tan45°=，则AD=100米，故AB=AD+BD=100(+1)米，选D． 如图，点A1、A2、A3、…、An在抛物线y=x2图象上，点B1、B2、B3、…、Bn在y轴上，若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形（点B0是坐标原点），则△A2015B2014B2015的腰长=____
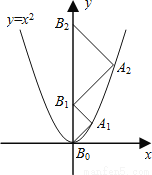
2015
【解析】作A1C⊥y轴，A2E⊥y轴，垂足分别为C、E．
∵△A1BOB1、△A2B1B2都是等腰直角三角形
∴B1C=B0C=DB0=A1D，B2E=B1E=A2E
∴设A1（a，a）将其代入解析式y=x2得：
∴a=a2
解得：a=0（不符合题意）或a=1，由勾股定理得：A1B0=
同理可以求得：A2B1=2
A3B2=3
A4B... 将进货单价为70元的某种商品按零售价100元一个售出时，每天能卖出20个，若这种商品的零售价每降价1元，其日销量就增加1个，为了获取每日最大利润，则应降价（ ）
A. 5元 B. 10元 C. 15元 D. 20元
A
【解析】设应降价x元，总利润为y元，根据题意可得：
，
化简、配方得：
，
∴当时，y最大=625，
∴ B、C、D错误，选A. 用一根长为50 cm的铁丝弯成一个长方形，设这个长方形的一边长为x（cm），它的面积为y（cm2），则y与x之间的函数关系式为（ ）
A. y＝－x2＋50x B. y＝x2－50x C. y＝－x2＋25x D. y＝－2x2＋25
C
【解析】设这个长方形的一边长为xcm，则另一边长为（25-x）cm，根据长方形的面积公式可得y=x（25-x）=－x2＋25x，故选C. 函数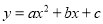
的图象如图，那么关于x的方程
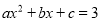的根的情况是（ ）
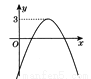
A. 有两个不相等的实数根 B. 有两个异号实数根
C. 有两个相等实数根 D. 无实数根
C
【解析】【解析】
将函数y=ax2+bx+c的图象往下平移3个单位即可得出函数y=ax2+bx+c﹣3的图象．∵函数y=ax2+bx+c的图象开口向下，顶点纵坐标为3，∴函数y=ax2+bx+c﹣3的图象与x轴只有一个交点，∴方程ax2+bx+c﹣3=0有两个相等的实数根．
故答案为：方程ax2+bx+c﹣3=0有两个相等的实数根． 身高相同的三个小朋友甲、乙、丙放风筝，他们放出的线长分别为300m，250 m，200m；线与地面所成的角度分别为30°，45°，60°(假设风筝线是拉直的)，则三人所放的风筝（ ）
A．甲的最高 B．乙的最低 C．丙的最低 D．乙的最高
D．
【解析】
试题解析：甲放的高度为：300×sin30°=150米．
乙放的高度为：250×sin45°=125≈176.75米．
丙放的高度为：200×sin60°=100≈173.2米．
所以乙的最高．
故选D．