��Ŀ����
ÿ�������·�������֦�������У�����ijˮ������5Ԫ/ǧ�˵ļ۸�һ����֦�������ۣ�����������������5%�����������0.7Ԫ/ǧ�ˣ����費���������ã�
��1��ˮ����Ҫ����֦�ۼ����ٶ�Ϊ���ٲŲ��������
��2�������۹����У�ˮ���̷���ÿ����֦��������m��ǧ�ˣ������۵���x��Ԫ/ǧ�ˣ�֮�������ϵ��m= -10x+120����ô�����۵��۶�Ϊ����ʱ��ÿ���õ�����w���
 ��1��ˮ����Ҫ����֦�ۼ����ٶ�Ϊ6Ԫ/ǧ�˲Ų��������2�������۵��۶�Ϊ9Ԫ/ǧ��ʱ��ÿ��ɻ�����w���
����������������1���蹺����֦aǧ�ˣ���֦�ۼ۶�ΪbԪ/ǧ��ʱ��ˮ����Ҫ�������������⽨������ʽ�����ֵ�Ϳ����ˣ�
��2���ɣ�1����֪��ÿǧ����֦��ƽ���ɱ�Ϊ6Ԫ���ٸ����ۼ�-����=����Ϳ��Ա�ʾ��w��Ȼ��Ϊ����ʽ�Ϳ��������ֵ��
���������
��1���蹺����֦aǧ�ˣ�...
��1��ˮ����Ҫ����֦�ۼ����ٶ�Ϊ6Ԫ/ǧ�˲Ų��������2�������۵��۶�Ϊ9Ԫ/ǧ��ʱ��ÿ��ɻ�����w���
����������������1���蹺����֦aǧ�ˣ���֦�ۼ۶�ΪbԪ/ǧ��ʱ��ˮ����Ҫ�������������⽨������ʽ�����ֵ�Ϳ����ˣ�
��2���ɣ�1����֪��ÿǧ����֦��ƽ���ɱ�Ϊ6Ԫ���ٸ����ۼ�-����=����Ϳ��Ա�ʾ��w��Ȼ��Ϊ����ʽ�Ϳ��������ֵ��
���������
��1���蹺����֦aǧ�ˣ�...
��x2+2��m��1��x+36����ȫƽ��ʽ����m=__��
 7��5
����������x2+2��m��1��x+36����ȫƽ��ʽ��
��2��m��1��x=��2��6x,
��m��1=��6,
��m=7��m=-5.
7��5
����������x2+2��m��1��x+36����ȫƽ��ʽ��
��2��m��1��x=��2��6x,
��m��1=��6,
��m=7��m=-5. ��֪��ABC�У�AB��AC����֤��B��90�㣬����д�����÷�֤��֤�������е��ĸ����裺�����ԡ�B����C����A��180�㣬�����������ڽǺͶ�����ì�ܣ������ԡ�B��90�㣻�ۼ����B��90�㣻����ô��AB��AC���á�B����C��90�㣬����B����C��180��.���ĸ�������ȷ��˳��Ӧ��_________(�����)��
 �ۢܢ٢�
��������������������÷�֤��������֤��ʱ�����ȼ�����۲�������Ȼ�������֪�����ó��붨����ì�ܣ����ó����費�������ó��𰸣�����ȷ������ǣ��ۢܢ٢ڣ�
�ۢܢ٢�
��������������������÷�֤��������֤��ʱ�����ȼ�����۲�������Ȼ�������֪�����ó��붨����ì�ܣ����ó����費�������ó��𰸣�����ȷ������ǣ��ۢܢ٢ڣ� ��ͼ��Сɽ������һ�ź���AB��ɽ��BC�����Ϊ30�㣬��Ϊ�˲�������AB��������Աѡ��ɽ��C��Ϊһ�����㣬�����������Ϊ45�㣬Ȼ��˳ɽ����������100����E�����ٲ����������Ϊ60�㣬������AB.������������� ��
��
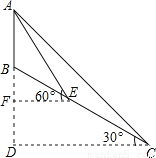
 ����AB��ԼΪ58��
����������������
������ɵã���AEB=30�㣬��ACE=15�㣬
�֡ߡ�AEB=��ACE+��CAE�����CAE=15�㡣
���ACEΪ���������Ρ���AE=CE=100�ס�
��Rt��AEF�У���AEF=60�㣬��EF=AEcos60��=50���ף���AF=AEsin60��=50���ף���
��Rt��BEF�У���BEF=30�㣬��BF=EFtan30��...
����AB��ԼΪ58��
����������������
������ɵã���AEB=30�㣬��ACE=15�㣬
�֡ߡ�AEB=��ACE+��CAE�����CAE=15�㡣
���ACEΪ���������Ρ���AE=CE=100�ס�
��Rt��AEF�У���AEF=60�㣬��EF=AEcos60��=50���ף���AF=AEsin60��=50���ף���
��Rt��BEF�У���BEF=30�㣬��BF=EFtan30��... ��һ������¥��¥����A��������Ľ�ѧ¥��̽������ʾ��������ѧ¥�ײ���C���ĸ���Ϊ45�㣬����¥������D��������Ϊ60�㣬��֪����¥֮���ˮƽ����Ϊ6�ף����ѧ¥�ĸ�CD�ǣ�������
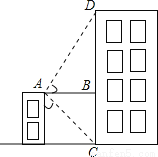
A����6+6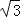 ���� B����6+3
���� B����6+3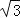 ���� C����6+2
���� C����6+2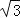 ���� D��12��
���� D��12��
 A
��������
�����������Rt��ACB�У���CAB=45�㣬AB��DC��AB=6��
��BC=AB=6��
��Rt��ABD����tan��BAD=��
��BD=AB•tan��BAD=6��
��DC=CB+BD=6+6��m����
��ѡA��
A
��������
�����������Rt��ACB�У���CAB=45�㣬AB��DC��AB=6��
��BC=AB=6��
��Rt��ABD����tan��BAD=��
��BD=AB•tan��BAD=6��
��DC=CB+BD=6+6��m����
��ѡA�� ��ͼ����֪����ֱ�ǡ�ABC��ֱ�DZ߳���������MNPQ�ı߳���Ϊ20���ף�AC��MN��ͬһֱ���ϣ���ʼʱ��A���N�غϣ��á�ABC��ÿ��2�����ٶ������˶������յ�A���M�غϣ����ص��������y������2����ʱ��t���룩֮��ĺ�����ϵʽΪ____
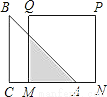
 y=��20-2t��2
��������AM=20-2t�����ص��������y=��AM2= ��20-2t��2
y=��20-2t��2
��������AM=20-2t�����ص��������y=��AM2= ��20-2t��2 ��ͼ��ʾ���Ź����������Σ��亯���ı���ʽΪy= -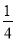 x2����ˮλ����ABλ��ʱ��ˮ���12m����ʱˮ�����Ŷ��ĸ߶�Ϊ��������
x2����ˮλ����ABλ��ʱ��ˮ���12m����ʱˮ�����Ŷ��ĸ߶�Ϊ��������
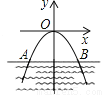
A. 3m B. 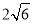 m C.
m C. 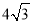 m D. 9 m
m D. 9 m
 D
���������������������֪֪��
��ĺ�����Ϊ.
�Ѵ���
��
��ˮ�����Ŷ��ĸ߶�Ϊ
��ѡD.
D
���������������������֪֪��
��ĺ�����Ϊ.
�Ѵ���
��
��ˮ�����Ŷ��ĸ߶�Ϊ
��ѡD. ��֪���κ���y=-x2+4x-3����ͼ����y�ύ�ڵ�B����x�ύ��A��C ����.���ABC���ܳ������.
 C��ABC=��S��ABC=3.
������������������ȷֱ���ö��κ�����ͼ����������Ľ������꣬�ٸ��ݹ��ɶ�����á�ABC�����߳������ɵõ���ABC���ܳ����ٸ��������ε������ʽ������ý��.
��x=0,��y=-3,��B������Ϊ(0,-3).
�ⷽ��-x2+4x-3=0,��x1=1,x2=3.
��A��C���������Ϊ(1,0),(3,0).
����AC=3-1=2,AB=,...
C��ABC=��S��ABC=3.
������������������ȷֱ���ö��κ�����ͼ����������Ľ������꣬�ٸ��ݹ��ɶ�����á�ABC�����߳������ɵõ���ABC���ܳ����ٸ��������ε������ʽ������ý��.
��x=0,��y=-3,��B������Ϊ(0,-3).
�ⷽ��-x2+4x-3=0,��x1=1,x2=3.
��A��C���������Ϊ(1,0),(3,0).
����AC=3-1=2,AB=,... ��ͼ��б��AC���¶ȣ��±ȣ�Ϊ1: 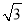 ��AC��10�ף��¶���һ��ֱ��ˮƽ������BC����˶���B����A����һ���ʴ�AB������AB��14�ף��������BC�ĸ߶ȣ�
��AC��10�ף��¶���һ��ֱ��ˮƽ������BC����˶���B����A����һ���ʴ�AB������AB��14�ף��������BC�ĸ߶ȣ�
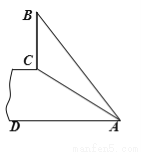
 6��.
��������
�������������ӳ�BC��AD��E�㣬��CE��AD��Ҫ��BC�ĸ߶ȣ���Ҫ֪��BE��CE�ĸ߶ȣ���Ҫ�����AE�ij��ȣ�ֱ��������ACE�����±ȣ���AC�ij�����ô�Ϳ����AE�ij���Ȼ�����BE��CE�ĸ߶ȣ�BC=BE-CE�����ɵó������
����������ӳ�BC��AD��E�㣬��CE��AD��
��Rt��AEC�У�AC=10�����±�Ϊ1����֪����CAE=30�㣬
��...
6��.
��������
�������������ӳ�BC��AD��E�㣬��CE��AD��Ҫ��BC�ĸ߶ȣ���Ҫ֪��BE��CE�ĸ߶ȣ���Ҫ�����AE�ij��ȣ�ֱ��������ACE�����±ȣ���AC�ij�����ô�Ϳ����AE�ij���Ȼ�����BE��CE�ĸ߶ȣ�BC=BE-CE�����ɵó������
����������ӳ�BC��AD��E�㣬��CE��AD��
��Rt��AEC�У�AC=10�����±�Ϊ1����֪����CAE=30�㣬
��... 
