如图，在△ABC中，∠B≠∠C.求证：AB≠AC.
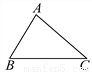
见解析
【解析】试题分析：首先假设AB=AC，从而得出与已知条件矛盾，从而得出答案．
试题解析：假设AB=AC， 则∠B=∠C，∴与已知矛盾，∴AB≠AC． 如图，已知在等边三角形ABC中，D、E分别是AB、AC上的点，且AD＝CE.求证：CD＝BE.
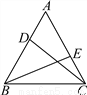
见解析
【解析】试题分析：首先根据等边三角形的性质得出∠A=∠BCE=60°，AC=BC，结合已知条件得出△ADC和△CEB全等，从而得出答案．
试题解析：∵△ABC为等边三角形， ∴∠A=∠BCE=60°，AC=BC，
又∵AD=CE， ∴△ADC≌△CEB(SAS)， ∴CD=BE． 等腰三角形是轴对称图形，它的对称轴是( )
A. 过顶点的直线 B. 底边上的高
C. 顶角的平分线所在的直线 D. 腰上的高所在的直线
C
【解析】等腰三角形的对称轴为顶角平分线所在的直线，
故选C． 下面四个图形中，不是轴对称图形的是（ ）
A. 有一个内角为45度的直角三角形 B. 有一个内角为60度的等腰三角形
C. 有一个内角为30度的直角三角形 D. 两个内角分别为36度和72度的三角形
C
【解析】A.有一个内角为45度的直角三角形，三个内角分别是45°、90°、45°，是等腰三角形，是轴对称图形；
B.有一个内角为60°的等腰三角形，三个角度数分别为60°、60°、60°，是等边三角形，是轴对称图形；对于C，有一个内角为30度的直角三角形，三个角度数分别为30°、90°、60°，不是等腰三角形，不是轴对称图形；
D.两个内角分别为36度和72度的三角形，三个角... 下列4个图形中，不是轴对称图形的是（ ）
A. 有2个内角相等的三角形 B. 有1个内角为30°的直角三角形
C. 有2个内角分别为30°和120°的三角形 D. 线段
B
【解析】A.有2个内角相等的三角形，是等腰三角形，是轴对称图形，不符合题意；
B.有1个内角为30°的直角三角形，三个角度数分别为30°、90°、60°，不是等腰三角形，故不是轴对称图形，符合题意；
C.有2个内角分别为30°和120°的三角形，三个角度数分别为30°、120°、30°，是等腰三角形，是轴对称图形，不符合题意；
D.线段是以其垂直平分线为对称轴，另一条对... 下列图形中，不一定是轴对称图形的是（ ）
A. 三角形 B. 射线 C. 角 D. 相交的两条直线
A
【解析】题中给出的四个选项中，射线以其所在直线为对称轴，角以其角平分线所在直线为对称轴，相交的两条直线以其夹角的平分线所在直线为对称轴.
故选：A. 下列图形中，不一定是轴对称图形的是（ ）
A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 等腰直角三角形
C
【解析】A.等腰三角形是轴对称图形，不符合题意；
B.等边三角形是轴对称图形，不符合题意；
C.直角三角形不一定是轴对称图形，符合题意；
D.等腰直角三角形是轴对称图形，不符合题意.
故选：C. 角、线段、三角形、圆、长方形和正方形中，一定是轴对称图形的有（ ）
A. 4个 B. 5个 C. 6个 D. 3个
B
【解析】通过分析可知，角、线段、圆、长方形和正方形都是轴对称图形，
故选：B. 等腰三角形、直角三角形、等边三角形、锐角三角形、钝角三角形和等腰直角三角形中，一定是轴对称图形的有（ ）
A. 3个 B. 4个 C. 5个 D. 2个
A
【解析】等腰三角形、等边三角形、等腰直角三角形都是轴对称图形，是轴对称图形的有3个.
故选：A. 下列字母中：H、F、A、O、M、W、Y、E，轴对称图形的个数是（ ）
A. 5 B. 4 C. 6 D. 7
D
【解析】从第一个字母研究，只要能够找到一条对称轴，令这个字母沿这条对称轴折叠后，两边的部分能够互相重合，就是轴对称图形，可以得出：字母H、A、O、M、W、Y、E这七个字母，属于轴对称图形.
故选：D.