题目内容
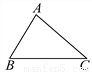
如图，在△ABC中，∠B≠∠C.求证：AB≠AC.
见解析
【解析】试题分析：首先假设AB=AC，从而得出与已知条件矛盾，从而得出答案．
试题解析：假设AB=AC， 则∠B=∠C，∴与已知矛盾，∴AB≠AC．
若将点A(1，3)向左平移2个单位，再向下平移4个单位得到B，则点B的坐标为( )
A. (－2，－1) B. (－1，0) C. (－1，－1) D. (－2，0)
C
【解析】∵点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，
∴点B的横坐标为1?2＝?1，纵坐标为3?4＝?1，
∴B的坐标为（?1，?1）．
故选C． 下列各式是完全平方式的是（ ）
A. x2+2x﹣1 B. 1+x2 C. x2+xy+1 D. x2﹣x+0.25
D
【解析】A. x2+2x﹣1两个平方项的符号不一致，不是完全平方式；
B. 1+x2缺少两倍的项，不是完全平方式；
C. x2+xy+1缺少两倍的项，不是完全平方式；
D. x2﹣x+0.25=(x-0.5)2,是完全平方式；
故选D. 如图，Rt△ABC中，∠C =90°，∠ABC的平分线BD交AC于D，若AD =5cm，CD =3cm，则点D到AB的距离DE是（ ）
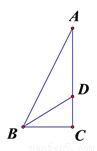
A. 5cm B. 4cm C. 3cm D. 2cm
C
【解析】∵点D到AB的距离是DE ，
∴DE⊥AB，
∵BD平分∠ABC，∠C =90°，
∴把Rt△BDC沿BD翻折后，点C在线段AB上的点E处，
∴DE=CD，
∵CD =3cm，
∴DE=3cm.
故选：C. 下列图形中，不一定是轴对称图形的是（ ）
A. 三角形 B. 射线 C. 角 D. 相交的两条直线
A
【解析】题中给出的四个选项中，射线以其所在直线为对称轴，角以其角平分线所在直线为对称轴，相交的两条直线以其夹角的平分线所在直线为对称轴.
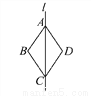
故选：A. 如图，四边形ABCD沿直线l对折后互相重合，如果AD∥BC，那么△ABC___(填“是”或“不是”)等腰三角形．
是
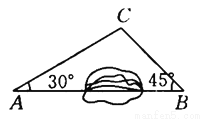
【解析】试题分析：根据折叠图形的性质可知：∠BAC=∠DAC，根据平行线的性质可知：∠DAC=∠ACB，则∠BAC=∠ACB，即△ABC为等腰三角形． 如图所示，A，B两地之间有一座山，汽车原来从A地到B地需要经C地沿折线A—C—B行驶，现开通隧道后，汽车直接沿直线AB行驶．已知AC＝10 km，∠A＝30°，∠B＝45°，则隧道开通后，汽车从A地到B地比原来少走多少千米?(结果精确到0.1 km,参考数据：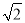 
≈1.41， 
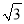≈1.73)
隧道开通后，汽车从A地到B地比原来少走约3.4 km
【解析】试题分析：过点C作AB的垂线CD，垂足为D，在直角△ACD和直角△CBD中，解直角三角形求出CD，AD，BC，就可以得到结论．
试题解析：过点C作AB的垂线CD，垂足为D．
∵AC=10km，∠A=30°，
∴CD=AC=5（km）．
AD==5（km）．
在Rt△CDB中，
∵∠B=45°，
... 已知：如图，直线y=3x+3与x轴交于C点，与y轴交于A点，B点在x轴上，△OAB是等腰直角三角形．
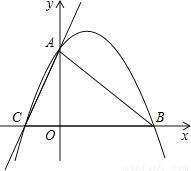
（1）求过A、B、C三点的抛物线的解析式；
（2）若P点是抛物线上的动点，且在第一象限，那么△PAB是否有最大面积？若有，求出此时P点的坐标和△PAB的最大面积；若没有，请说明理由．
（1）y= -x2+2x+3（2）存在,（）
【解析】试题分析：（1）求得直线y=3x+3与坐标轴的两交点坐标，然后根据OB=OA即可求得点B的坐标，然后利用待定系数法求得经过A、B、C三点的抛物线的解析式即可；
（2）首先利用待定系数法求得直线AB的解析式，然后根据CD∥AB得到两直线的k值相等，根据直线CD经过点C求得直线CD的解析式，然后求得直线CD和抛物线的交点坐标即可；
... 根据下列表格的对应值：
判断方程 ax2＋bx＋c=0(a≠0，a，b，c为常数)的一个解x的取值范围是( )
A. 3＜x＜3.23 B. 3．23＜x＜3.24 C. 3.24＜x＜3.25 D. 3.25＜x＜3.26
C
【解析】【解析】
函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根，函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0；
由表中数据可知：y=0在y=﹣0.02与y=0.03之间，∴对应的x的值在3.24与3.25之间，即3.24＜x＜3.25．故选C．