如图所示，已知AD∥BC，要使四边形ABCD为平行四边形，需要增加的条件是________．(只需填一个你认为正确的条件即可).
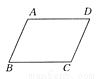
AD＝BC，或AB∥AD(答案不唯一)
【解析】【解析】
根据平行四边形的判定方法，需要增加的条件是：AD=BC或AB∥CD或∠A=∠C或∠B=∠D．故答案为：AD=BC（或AB∥CD）． 一个四边形的边长依次是a，b，c，d，且a2＋b2＋c2＋d2＝2ac＋2bd，则这个四边形是______，依据是________．
平行四边形 两组对边分别相等的四边形是平行四边形
【解析】【解析】
a2+b2+c2+d2=2ac+2bd，（a2﹣2ac+c2）+（b2﹣2bd+d2）=0，（a﹣c）2+（b﹣d）2=0，∴a﹣c=0，b﹣d=0，∴a=c，b=d，∴四边形是平行四边形（两组对边分别相等的四边形是平行四边形）．故答案为：平行四边形，两组对边分别相等的四边形是平行四边形． 如图所示，已知D，E，F分别在△ABC的边BC，AB，AC上，且DE∥AF，DE＝AF，将FD延长至G，使FG＝2DF，连接AG，则ED，AG互相平分吗?请说明理由．
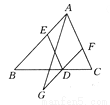
互相平分
【解析】试题分析：求ED与AG互相平分，只要证明四边形AEGD是平行四边形即可解答，由DE∥AC，DE=AF，可得四边形AEDF是平行四边形，所以，AE∥DF且AE=DF，又FG=2DF，则AE=GD，所以，四边形AEGD是平行四边形，即可得出ED与AG互相平分．
试题解析：证明：如图，连接AD，GE，∵DE∥AC，DE=AF，∴四边形AEDF是平行四边形，∴AE∥DF且AE... 已知某个平行四边形的一边长为7，一条对角线长为8，求另一条对角线长的取值范围．
6＜x＜22．
【解析】试题分析：由平行四边形的对角线互相平分，根据三角形三边之间的关系，可先求得另一对角线的一半的取值范围，进而可求出这条对角线的范围．
试题解析：【解析】
如图，已知平行四边形中，AB=7，AC=8．由题意得，BD=2OB，AC=2OA=8，∴OB=BD，OA=4．在△AOB中，AB﹣OA＜OB＜AB+OA，可得3＜OB＜11，即6＜BD＜22．故答案为：6＜BD... 如图所示，在
ABCD中，E，F，G，H分别是四条边上的点，且满足AE＝CF，BG＝DH，连接EF，GH．试说明EF和GH互相平分．
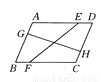
答案见解析
【解析】试题分析：如图，连接EG，GF，FH，HE，证明四边形EGFH是平行四边形，问题即可解决．
试题解析：【解析】
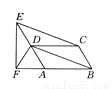
连接EG，GF，FH，HE．如图，∵四边形ABCD为平行四边形，∴∠B＝∠D，AD＝BC．又∵AE＝CF，∴AD－AE＝BC－CF，即DE=BF．又∵DH＝BG，∴△BFG≌△DEH(SAS)，∴GF＝EH，同理GE=FH，∴四边形EGFH平行四边形，∴... 如图所示，在
ABCD中，CE∥BD，EF⊥AB交BA延长线于点F，E，D，A在一条直线上，那么有DF＝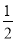
AE，请你说明理由．(提示：直角三角形中斜边中线等于斜边的一半)
答案见解析
【解析】试题分析：首先根据平行四边形的性质可得AD=BC，AD∥BC，再证明四边形EDBC是平行四边形，可得ED=CB，然后根据直角三角形斜边上的中线等于斜边的一半可得结论．
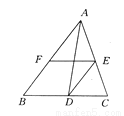
试题解析：证明：∵四边形ABCD为平行四边形，∴AD=BC，AD∥BC．∵CE∥BD，∴四边形EDBC是平行四边形，∴ED=CB，∴ED=AD．∵EF⊥AB，∴△EFA是直角三角形，∴DF=AE． 如图所示，AD为△ABC的一条角平分线，E，F分别在AC，AB上，DE∥AB，BF＝AE．试说明EF＝BD．
答案见解析
【解析】试题分析：由角平分线的定义和平行线的性质可证明∠ADE=∠CAD，可得AE=DE，结合条件可证明四边形EFBD为平行四边形，可得EF=BD．
试题解析：证明：∵AD平分∠BAC，∴∠BAD=∠CAD．∵DE∥AB，∴∠BAD=∠ADE，∴∠CAD=∠ADE，∴AE=DE．又∵BF=AE，∴DE=BF．又∵DE∥AB，∴四边形EFBD是平行四边形，∴EF=BD．
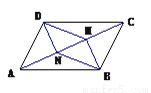
... 如图，AC是□ABCD的一条对角线，BM⊥AC， DN⊥AC，垂足分别为M，N，四边形BMDN是平行四边形吗?请选择一种你认为比较好的方法证明．
答案见解析
【解析】试题分析：由四边形ABCD是平行四边形，可得AD=BC，AD∥BC，又由BM⊥AC，DN⊥AC，即可得BM∥DN，∠DNA=∠BMC=90°，然后利用AAS证得△ADN≌△CBM，即可得DN=BM，由有一组对边相等且平行的四边形是平行四边形，即可证得四边形BMDN是平行四边形．
试题解析：【解析】
四边形BMDN是平行四边形．理由如下：
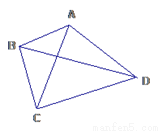
∵四边形ABCD是平... 如图，为公园的一块草坪，其四角上各有一棵树，现园林工人想使这个草坪的面积扩大一倍，又要四棵树不动，并使扩大后的草坪为平行四边形，试问这个想法能否实现，若能请你设计出草图，否则说明理由．
答案见解析
【解析】试题分析：过A、C，B、D分别作BD，AC的平行线，且这些平行线两两相交于E、F、G、H，从而EAOB、BOCF、OCGD、AODH都是平行四边形，利用平行四边形的对角线将平行四边形的面积分为相等的两块，可知ABCD的面积是EFGH面积的一半．
试题解析：【解析】
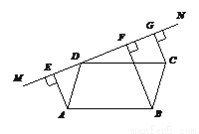
如图所示，过A、C，B、D分别作BD，AC的平行线，且这些平行线两两相交于E、F、G、H，则四边形E... 如图，直线MN过□ABCD的顶点D，过A，B，C三点，分别作MN的垂线，垂足分别是E，F，G．
求证：DE＝FG．
答案见解析
【解析】试题分析：作CH⊥BF与H．可证△AED≌△BHC，得到ED=HC，再由平行线间的距离处处相等得到FG=CH，即可得到结论．
试题解析：证明：作CH⊥BF与H．
∵AE⊥MN，BF⊥MN，∴AE∥BF，∴∠EAD+∠DAB+∠ABF=180°．
∵ABCD是平行四边形，∴AD∥BC，AD=BC，∴∠DAB+∠ABF+∠HBC=180°，∴∠EAD=∠HB...