题目内容
已知某个平行四边形的一边长为7,一条对角线长为8,求另一条对角线长的取值范围.
 6<x<22.
【解析】试题分析:由平行四边形的对角线互相平分,根据三角形三边之间的关系,可先求得另一对角线的一半的取值范围,进而可求出这条对角线的范围.
试题解析:【解析】
如图,已知平行四边形中,AB=7,AC=8.由题意得,BD=2OB,AC=2OA=8,∴OB=BD,OA=4.在△AOB中,AB﹣OA<OB<AB+OA,可得3<OB<11,即6<BD<22.故答案为:6<BD...
6<x<22.
【解析】试题分析:由平行四边形的对角线互相平分,根据三角形三边之间的关系,可先求得另一对角线的一半的取值范围,进而可求出这条对角线的范围.
试题解析:【解析】
如图,已知平行四边形中,AB=7,AC=8.由题意得,BD=2OB,AC=2OA=8,∴OB=BD,OA=4.在△AOB中,AB﹣OA<OB<AB+OA,可得3<OB<11,即6<BD<22.故答案为:6<BD...
练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
如图所示的抛物线是二次函数y= +bx+c(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b,其中正确的结论有( ).
+bx+c(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b,其中正确的结论有( ).
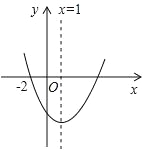
A.1个 B.2个 C.3个 D.4个
 C.
【解析】
试题分析:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x==1,∴b=﹣2a<0,所以②正确;∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,所以①正确;∵点(﹣2,0)关于直线x=1的对称点的坐标为(4,0),∴抛物线与x轴的另一个交点坐标为(4,0),所以③正确;∵x=﹣1时,y<0,
即a﹣b+c<0,∴a+c<b,所以④错误.
故选:C...
C.
【解析】
试题分析:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x==1,∴b=﹣2a<0,所以②正确;∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,所以①正确;∵点(﹣2,0)关于直线x=1的对称点的坐标为(4,0),∴抛物线与x轴的另一个交点坐标为(4,0),所以③正确;∵x=﹣1时,y<0,
即a﹣b+c<0,∴a+c<b,所以④错误.
故选:C... 下列结论中,正确的是( )
A. 若a>b,则 <
<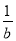 B. 若a>b,则a2>b2
B. 若a>b,则a2>b2
C. 若a>b,则1-a<1-b D. 若a>b,ac2>bc2
 C
【解析】当1>a>b>0时, <,故不正确;当a>0,b<0,a<|b|时,a2<b2,故不正确;由a>b可知-a<-b,因此可得1-a<1-b,故正确;当c=0时,虽然a>b,但是ac2=bc2=0,故不正确.
故选:C.
C
【解析】当1>a>b>0时, <,故不正确;当a>0,b<0,a<|b|时,a2<b2,故不正确;由a>b可知-a<-b,因此可得1-a<1-b,故正确;当c=0时,虽然a>b,但是ac2=bc2=0,故不正确.
故选:C. 在□ABCD中,对角线AC,BD相交于O点,AC=10,BD=8,则AD长的取值范围是 ( )
A. AD>1 B. AD<9 C. 1<AD<9 D. AD>10
 C
【解析】【解析】
平行四边形的对角线互相平分得:两条对角线的一半分别是5,4.再根据三角形的三边关系,得:1<AD<9.故选C.
C
【解析】【解析】
平行四边形的对角线互相平分得:两条对角线的一半分别是5,4.再根据三角形的三边关系,得:1<AD<9.故选C. 如图,为公园的一块草坪,其四角上各有一棵树,现园林工人想使这个草坪的面积扩大一倍,又要四棵树不动,并使扩大后的草坪为平行四边形,试问这个想法能否实现,若能请你设计出草图,否则说明理由.
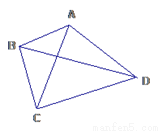
 答案见解析
【解析】试题分析:过A、C,B、D分别作BD,AC的平行线,且这些平行线两两相交于E、F、G、H,从而EAOB、BOCF、OCGD、AODH都是平行四边形,利用平行四边形的对角线将平行四边形的面积分为相等的两块,可知ABCD的面积是EFGH面积的一半.
试题解析:【解析】
如图所示,过A、C,B、D分别作BD,AC的平行线,且这些平行线两两相交于E、F、G、H,则四边形E...
答案见解析
【解析】试题分析:过A、C,B、D分别作BD,AC的平行线,且这些平行线两两相交于E、F、G、H,从而EAOB、BOCF、OCGD、AODH都是平行四边形,利用平行四边形的对角线将平行四边形的面积分为相等的两块,可知ABCD的面积是EFGH面积的一半.
试题解析:【解析】
如图所示,过A、C,B、D分别作BD,AC的平行线,且这些平行线两两相交于E、F、G、H,则四边形E... BD是□ABCD的对角线,点E,F在BD上,要使四边形AECF是平行四边形,还需添加的条件是______(只添一个你认为正确的即可).
 BE=DF等
【解析】【解析】
如图,连接AC交BD于点O.
∵四边形ABCD为平行四边形,∴AO=CO,BO=DO,∴当BE=DF时,可得OE=OF,则四边形AECF为平行四边形,∴可增加BE=DF.故答案为:BE=DF(答案不唯一).
BE=DF等
【解析】【解析】
如图,连接AC交BD于点O.
∵四边形ABCD为平行四边形,∴AO=CO,BO=DO,∴当BE=DF时,可得OE=OF,则四边形AECF为平行四边形,∴可增加BE=DF.故答案为:BE=DF(答案不唯一). 不能判断四边形ABCD是平行四边形的是( )
A. AB=CD,AD=BC B. AB=CD,AB∥CD
C. AB=CD,AD∥BC D. AB∥CD,AD∥BC
 C
【解析】平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.∴C能判断,
平行四边形判定定理1,两组对角分别相等的四边形是平行四边形;∴B能判断;
平行四边形判定定理2,两组对边分别相等的四边形是平行四边形;∴D能判定;
平行四边形判定定理3,对角线互相平分的四边形是平行四边形;
平行四边形判定定理4,一组对边平行相等的四边形是平行四边形;
故选A.
...
C
【解析】平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.∴C能判断,
平行四边形判定定理1,两组对角分别相等的四边形是平行四边形;∴B能判断;
平行四边形判定定理2,两组对边分别相等的四边形是平行四边形;∴D能判定;
平行四边形判定定理3,对角线互相平分的四边形是平行四边形;
平行四边形判定定理4,一组对边平行相等的四边形是平行四边形;
故选A.
... 若不等式(a-2)x>a-2可以变形为x<1,则a的取值范围为_____.
 a<2
【解析】根据一元一次不等式的解法和基本性质,可由(a-2)x>a-2的解集为x<1,可知a-2<0,解得a<2.
故答案为:a<2.
a<2
【解析】根据一元一次不等式的解法和基本性质,可由(a-2)x>a-2的解集为x<1,可知a-2<0,解得a<2.
故答案为:a<2. 化简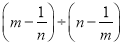 的结果是( )
的结果是( )
A. 1 B. 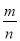 C.
C. 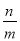 D. -1
D. -1
 B
【解析】试题分析:
=
=
=.
故选B.
B
【解析】试题分析:
=
=
=.
故选B. 
