题目内容
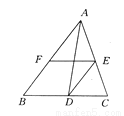
如图所示,AD为△ABC的一条角平分线,E,F分别在AC,AB上,DE∥AB,BF=AE.试说明EF=BD.
 答案见解析
【解析】试题分析:由角平分线的定义和平行线的性质可证明∠ADE=∠CAD,可得AE=DE,结合条件可证明四边形EFBD为平行四边形,可得EF=BD.
试题解析:证明:∵AD平分∠BAC,∴∠BAD=∠CAD.∵DE∥AB,∴∠BAD=∠ADE,∴∠CAD=∠ADE,∴AE=DE.又∵BF=AE,∴DE=BF.又∵DE∥AB,∴四边形EFBD是平行四边形,∴EF=BD.
...
答案见解析
【解析】试题分析:由角平分线的定义和平行线的性质可证明∠ADE=∠CAD,可得AE=DE,结合条件可证明四边形EFBD为平行四边形,可得EF=BD.
试题解析:证明:∵AD平分∠BAC,∴∠BAD=∠CAD.∵DE∥AB,∴∠BAD=∠ADE,∴∠CAD=∠ADE,∴AE=DE.又∵BF=AE,∴DE=BF.又∵DE∥AB,∴四边形EFBD是平行四边形,∴EF=BD.
...
练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
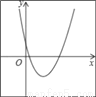
二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过( )
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
 C
【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.
故选C.
C
【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.
故选C. 不等式组 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( )
A. 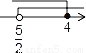 B.
B. 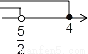 C.
C. 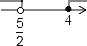 D.
D. 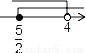
 A
【解析】解不等式x-1≤7-x得x≤4;
解不等式5x-2>3(x+1)得x>,
所以<x≤4.
在数轴上表示正确的是A.
故选A.
A
【解析】解不等式x-1≤7-x得x≤4;
解不等式5x-2>3(x+1)得x>,
所以<x≤4.
在数轴上表示正确的是A.
故选A. 在等腰梯形ABCD中,AD∥BC,AE⊥BC于E,且AE=AD,BC=3AE, 则∠BAD等于 ( )
A. 120° B. 135° C. 130° D. 不能确定
 B
【解析】【解析】
过点D作DF⊥BC于点F.
∵AE⊥BC,DF⊥BC,AD=AE,∴四边形AEFD为正方形,∴AD=EF.
∵AD=AE,BC=3AD,∴BE=AE=EF=FC,∴∠B=45°,∴∠BAD=135°.
故选B.
B
【解析】【解析】
过点D作DF⊥BC于点F.
∵AE⊥BC,DF⊥BC,AD=AE,∴四边形AEFD为正方形,∴AD=EF.
∵AD=AE,BC=3AD,∴BE=AE=EF=FC,∴∠B=45°,∴∠BAD=135°.
故选B. 平行四边行的两条对角线把它分成全等三角形的对数是( )
A. 2 B. 4 C. 6 D. 8
 B
【解析】【解析】
如图,?ABCD中,AC,DB分别分得△ABC≌△CDA,△ABD≌△CDB,
又对角线互相平分得到△AOD≌△COB,△AOB≌△COD,所以有4对.
故选B.
B
【解析】【解析】
如图,?ABCD中,AC,DB分别分得△ABC≌△CDA,△ABD≌△CDB,
又对角线互相平分得到△AOD≌△COB,△AOB≌△COD,所以有4对.
故选B. 一个四边形的边长依次是a,b,c,d,且a2+b2+c2+d2=2ac+2bd,则这个四边形是______,依据是________.
 平行四边形 两组对边分别相等的四边形是平行四边形
【解析】【解析】
a2+b2+c2+d2=2ac+2bd,(a2﹣2ac+c2)+(b2﹣2bd+d2)=0,(a﹣c)2+(b﹣d)2=0,∴a﹣c=0,b﹣d=0,∴a=c,b=d,∴四边形是平行四边形(两组对边分别相等的四边形是平行四边形).故答案为:平行四边形,两组对边分别相等的四边形是平行四边形.
平行四边形 两组对边分别相等的四边形是平行四边形
【解析】【解析】
a2+b2+c2+d2=2ac+2bd,(a2﹣2ac+c2)+(b2﹣2bd+d2)=0,(a﹣c)2+(b﹣d)2=0,∴a﹣c=0,b﹣d=0,∴a=c,b=d,∴四边形是平行四边形(两组对边分别相等的四边形是平行四边形).故答案为:平行四边形,两组对边分别相等的四边形是平行四边形. 在□ABCD中,AB≠AD,满足下列条件,不一定能构成平行四边形的是( )
A. 四个内角平分线围成的四边形
B. 过四个顶点作对边的高线围成的四边形
C. 以对角线的交点把对角线分成的四部分的中点为顶点的四边形
D. 以一条对角线上的两点,与另两个顶点为顶点的四边形.
 D
【解析】【解析】
∵?ABCD的四个内角平分线围成的四边形是平行四边形,∴选项A正确;
∵过?ABCD四个顶点作对边的高线围成的四边形是平行四边形,∴选项B正确;
∵以?ABCD各边中点为顶点的四边形是平行四边形,∴选项C正确;
∵以?ABCD一条对角线上的两点与另两个顶点为顶点的四边形不一定是平行四边形,∴选项D不正确.
故选D.
D
【解析】【解析】
∵?ABCD的四个内角平分线围成的四边形是平行四边形,∴选项A正确;
∵过?ABCD四个顶点作对边的高线围成的四边形是平行四边形,∴选项B正确;
∵以?ABCD各边中点为顶点的四边形是平行四边形,∴选项C正确;
∵以?ABCD一条对角线上的两点与另两个顶点为顶点的四边形不一定是平行四边形,∴选项D不正确.
故选D. 不等式2x<7的解有_____个,其中非负整数解有___个.
 无数 4
【解析】解不等式2x<7可得x<,所以不等式有无数各界,其中非负整数解有0、1、2、3,共4个.
故答案为:无数,4.
无数 4
【解析】解不等式2x<7可得x<,所以不等式有无数各界,其中非负整数解有0、1、2、3,共4个.
故答案为:无数,4. 计算
(1) (2)
(2)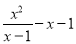
(3)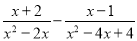 (4)
(4)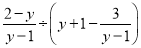
 (1);(2);(3);(4).
【解析】试题分析:(1)同分母分式相减,分母不变,把分子相减,最后结果化成最简即可;
(2)把整式看成是分母为1的分式,通分后把分子相减即可;
(3)把两个分母分解因式后通分,再利用同分母分式减法法则进行计算即可;
(4)把括号内的分式通分相减,化成最简后,再把除法转化为乘法,分母分解因式后再进行约分即可.
试题解析:
【解析】...
(1);(2);(3);(4).
【解析】试题分析:(1)同分母分式相减,分母不变,把分子相减,最后结果化成最简即可;
(2)把整式看成是分母为1的分式,通分后把分子相减即可;
(3)把两个分母分解因式后通分,再利用同分母分式减法法则进行计算即可;
(4)把括号内的分式通分相减,化成最简后,再把除法转化为乘法,分母分解因式后再进行约分即可.
试题解析:
【解析】... 
