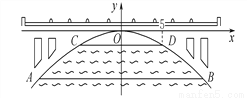
如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为20m，如果水位上升3m时，水面CD的宽是10m，建立如图所示的直角坐标系，则此抛物线的解析式为___________．
y＝－x2
【解析】【解析】
设抛物线解析式为y=ax2，因为抛物线关于y轴对称，AB=20，所以点B的横坐标为10．设点B（10，n），点D（5，n+3），由题意得： ，解得： ，∴．
故答案为： ． 如图，教练对小明推铅球的录像进行技术分析，发现铅球行进高度y(m)与水平距离x(m)之间的关系为y＝－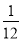
(x－4)2＋3，由此可知铅球推出的距离是___________.
10
【解析】【解析】
在中，令y=0，得，解得：x1=10，x2=﹣2（舍去），即铅球推出的距离是10m．故答案为：10． 若抛物线y=x2+bx+c与x轴只有一个交点，且过点A（m，n），B（m+6，n），则n= ．
9
【解析】
分析：∵抛物线y=x2+bx+cx轴只有一个交点，∴当时，y=0．且b2﹣4c=0，即b2=4c．
又∵点A（m，n），B（m+6，n），∴点A、B关于直线对称。
∴A（，n），B（，n）。
将A点坐标代入抛物线解析式，得：。 已知抛物线y＝x2－mx＋m－2.
(1)求证此抛物线与x轴有两个交点；
(2)若抛物线与x轴的一个交点为(2，0)，求m的值及抛物线与x轴另一交点坐标．
(1)证明见解析(2)抛物线与x轴另一交点坐标为(0，0)
【解析】试题分析：（1）欲证明抛物线与x轴有两个不同的交点，只要证明△＞0即可．
（2）把(2，0)代入抛物线解析式，即可得到m的值，从而得到抛物线的解析式，令y=0，解方程即可得到结论．
试题解析：【解析】
(1)∵Δ＝(－m)2－4(m－2)＝m2－4m＋8＝(m－2)2＋4＞0， ∴此抛物线与x轴有两个交点．
... 今年，6月12日为端午节．在端午节前夕，三位同学到某超市调研一种进价为2元的粽子的销售情况．请根据小丽提供的信息，解答小华和小明提出的问题．
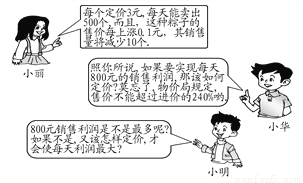
(1)当定价为4元时，能实现每天800元的销售利润(2)当定价为4.8元时，每天的销售利润最大．
【解析】试题分析：（1）小华的问题要用一元二次方程来解决，解答的关键是弄清：设实现每天800元利润的定价为x元/个时，每一个粽子的利润为（x-2）元，一共能卖（500-×10）个粽子，根据题意列方程得：（x-2)（500-×10）=800，解得x1=4,x2=6，还应根据实际问题确定两个值是否都... 如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成，已知河底ED是水平的，ED＝16m，AE＝8m，抛物线的顶点C到ED的距离是11m，以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系．
(1)求抛物线的解析式；
(2)已知从某时刻开始的40h内，水面与河底ED的距离h(单位：m)随时间t(单位：h)的变化满足函数关系h＝－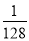
(t－19)2＋8(0≤t≤40)且当水面到顶点C的距离不大于5m时，需禁止船只通行，请通过计算说明：在这一时段内，需多少小时禁止船只通行？
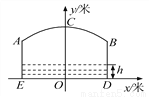
(1)y＝－x2＋11(2)禁止船只通行时间为32小时．
【解析】二次函数的应用，待定系数法，曲线上点的坐标与方程的关系。
（1）根据抛物线特点设出二次函数解析式，把B坐标代入即可求解。
（2）水面到顶点C的距离不大于5米时，即水面与河底ED的距离h至多为6，把6代入所给二次函数关系式，求得t的值，相减即可得到禁止船只通行的时间。 抛物线y=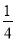
x2+bx+c与x轴交于A(5,0)、B(-1,0)两点，过点A作直线AC⊥x轴，交直线y=2x于点C.
（1）求该抛物线的解析式；
（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；
（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由.
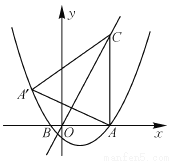
（1）．（2）点A/的坐标为（﹣3,4）．点A/在该抛物线上．（3）点P运动到时，四边形PACM是平行四边形．
【解析】试题分析：（1）将点A、B的坐标代入抛物线的解析式，得到关于b、c的二元一次方程组，从而可解得b、c的值；
（2）过点B′作B′E⊥x轴于E，BB′与OC交于点F．由平行于y轴的直线上各点横坐标相同可知点C的横坐标为2，将x=2代入直线y=﹣2x的解析式可求得点C的坐... 在下列y关于x的函数中，一定是二次函数的是（ ）
A. y=2x2 B. y=2x﹣2 C. y=ax2 D.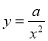 
A
【解析】解：A．是二次函数，故A符合题意；
B．是一次函数，故B错误；
C．a=0时，不是二次函数，故C错误；
D．a≠0时是分式方程，故D错误；
故选A． 已知二次函数y=﹣2x2+4x﹣3，如果y随x的增大而减小，那么x的取值范围是（ ）
A. x≥1 B. x≥0 C. x≥﹣1 D. x≥﹣2
A
【解析】【解析】
∵y=﹣2x2+4x﹣3=﹣2（x﹣1）2﹣1，∴抛物线开口向下，对称轴为x=1，∴当x≥1时，y随x的增大而减小．故选A． 下列抛物线中，与抛物线y=x2﹣2x+4具有相同对称轴的是（ ）
A. y=4x2+2x+1 B. y=2x2﹣4x+1 C. y=2x2﹣x+4 D. y=x2﹣4x+2
B
【解析】【解析】
抛物线y=x2﹣2x+4的对称轴为x=1；
A、y=4x2+2x+1的对称轴为x=﹣，不符合题意；
B、y=2x2﹣4x+1的对称轴为x=1，符合题意；
C、y=2x2﹣x+4的对称轴为x=，不符合题意；
D、y=x2﹣4x+2的对称轴为x=2，不符合题意；
故选B．