题目内容
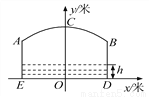
如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成，已知河底ED是水平的，ED＝16m，AE＝8m，抛物线的顶点C到ED的距离是11m，以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系．
(1)求抛物线的解析式；
(2)已知从某时刻开始的40h内，水面与河底ED的距离h(单位：m)随时间t(单位：h)的变化满足函数关系h＝－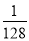
(t－19)2＋8(0≤t≤40)且当水面到顶点C的距离不大于5m时，需禁止船只通行，请通过计算说明：在这一时段内，需多少小时禁止船只通行？
(1)y＝－x2＋11(2)禁止船只通行时间为32小时．
【解析】二次函数的应用，待定系数法，曲线上点的坐标与方程的关系。
（1）根据抛物线特点设出二次函数解析式，把B坐标代入即可求解。
（2）水面到顶点C的距离不大于5米时，即水面与河底ED的距离h至多为6，把6代入所给二次函数关系式，求得t的值，相减即可得到禁止船只通行的时间。
名校通行证有效作业系列答案已知：如图，在四边形ABCD中，AB∥CD，E是BC的中点，直线AE交DC的延长线于点F．试判断四边形ABFC的形状，并证明你的结论．
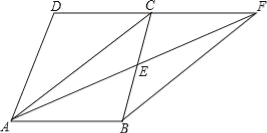
四边形ABFC是平行四边形；证明见解析.
【解析】
试题分析：易证△ABE≌△FCE（AAS），然后利用一组对边平行且相等可判断四边形ABFC是平行四边形.
试题解析：四边形ABFC是平行四边形；理由如下：∵AB∥CD，∴∠BAE=∠CFE，∵E是BC的中点，
∴BE=CE，在△ABE和△FCE中，，∴△ABE≌△FCE（AAS）；∴AB=CF，又∵AB∥CF，∴四边形AB... 若一个正n边形的每个内角为144°，则这个正n边形的所有对角线的条数是（ ）
A. 7 B. 10 C. 35 D. 70
C
【解析】由正n边形的每个内角为144°结合多边形内角和公式，即可得出关于n的一元一次方程，解方程即可求出n的值，将其代入中即可得出结论．
【解析】
∵一个正n边形的每个内角为144°，
∴144n=180×（n﹣2），解得：n=10．
这个正n边形的所有对角线的条数是：==35．
故选C． 如图，抛物线y=﹣x2+2x+3与y轴交于点C，点D（0，1），点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为 ．
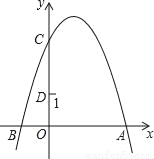
（1+，2）或（1﹣，2）．
【解析】【解析】
∵△PCD是以CD为底的等腰三角形，∴点P在线段CD的垂直平分线上，如图，过P作PE⊥y轴于点E，则E为线段CD的中点，∵抛物线与y轴交于点C，∴C（0，3），且D（0，1），∴E点坐标为（0，2），∴P点纵坐标为2，在中，令y=2，可得，解得x=，∴P点坐标为（，2）或（，2），故答案为：（，2）或（，2）． 将抛物线y=ax2﹣1平移后与抛物线y=a（x﹣1）2重合，抛物线y=ax2﹣1上的点A（2，3）同时平移到A′，那么点A′的坐标为（ ）
A. （3，4） B. （1，2） C. （3，2） D. （1，4）
A
【解析】【解析】
∵抛物线y=ax2﹣1的顶点坐标是（0，﹣1），抛物线y=a（x﹣1）2的顶点坐标是（1，0），∴将抛物线y=ax2﹣1向右平移1个单位，再向上平移1个单位得到抛物线y=a（x﹣1）2，∴将点A（2，3）向右平移1个单位，再向上平移1个单位得到点A′的坐标为（3，4）．
故选A． 如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为20m，如果水位上升3m时，水面CD的宽是10m，建立如图所示的直角坐标系，则此抛物线的解析式为___________．
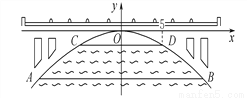
y＝－x2
【解析】【解析】
设抛物线解析式为y=ax2，因为抛物线关于y轴对称，AB=20，所以点B的横坐标为10．设点B（10，n），点D（5，n+3），由题意得： ，解得： ，∴．
故答案为： ． 已知二次函数y＝x2－3x＋m(m为常数)的图象与x轴的一个交点为(1，0)，则关于x的一元二次方程x2－3x＋m＝0的两实数根是( )
A. x1＝1，x2＝－1 B. x1＝1，x2＝2 C. x1＝1，x2＝0 D. x1＝1，x2＝3
B
【解析】试题分析：关于x的一元二次方程x2-3x+m=0的两实数根就是二次函数y=x2-3x+m（m为常数）的图象与x轴的两个交点的横坐标．∵二次函数的解析式是y=x2-3x+m（m为常数），∴该抛物线的对称轴是：x=．
又∵二次函数y=x2-3x+m（m为常数）的图象与x轴的一个交点为（1，0），
∴根据抛物线的对称性质知，该抛物线与x轴的另一个交点的坐标是（2，0），
... 如图所示为一个污水净化塔内部，污水从上方入口进入后，流经形如等腰直角三角形的净化材枓表面，流向如图中箭头所示，每一次水流流经三角形两腰的机会相同，经过四层净化后流入底部的5个出口中的一个．下列判断：①5个出口的出水量相同；②2号出口的出水量与4号出口的出水量相同；③1，2，3号出水口的出水量之比约为1：4：6；④若净化材枓损耗的速度与流经其表面水的数量成正比，则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍．其中正确的判断有（ ）个．
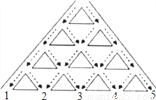
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】根据出水量假设出第一次分流都为1，可以得出下一次分流的水量，依此类推得出最后得出每个出水管的出水量，进而得出答案．
【解析】
根据图示可以得出：
①根据图示出水口之间存在不同，故此选项错误；
②2号出口的出水量与4号出口的出水量相同；
根据第二个出水口的出水量为： +=，
第4个出水口的出水量为： +=，
故此选项正确；
③1，2，3号... 以下是回收、绿色包装、节水、低碳四个标志，其中是中心对称图形的是（ ）
A. 
B. 
C. 
D. 
B
【解析】试题解析：A、不是中心对称图形，本选项错误；
B、是中心对称图形，本选项正确；
C、不是中心对称图形，本选项错误；
D、不是中心对称图形，本选项错误．
故选B．