��Ŀ����
������y=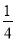 x2+bx+c��x�ύ��A(5,0)��B(-1,0)���㣬����A��ֱ��AC��x�ᣬ��ֱ��y=2x�ڵ�C.
x2+bx+c��x�ύ��A(5,0)��B(-1,0)���㣬����A��ֱ��AC��x�ᣬ��ֱ��y=2x�ڵ�C.
��1����������ߵĽ���ʽ��
��2�����A����ֱ��y=2x�ĶԳƵ�A������꣬�ж���A���Ƿ����������ϣ���˵�����ɣ�
��3����P����������һ���㣬����P��y���ƽ���ߣ����߶�CA���ڵ�M���Ƿ���������ĵ�P��ʹ�ı���PACM��ƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ���˵������.
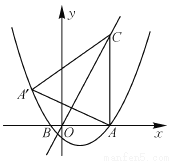
 ��1������2����A/������Ϊ����3,4������A/�ڸ��������ϣ���3����P�˶���ʱ���ı���PACM��ƽ���ı��Σ�
�������������������1������A��B��������������ߵĽ���ʽ���õ�����b��c�Ķ�Ԫһ�η����飬�Ӷ��ɽ��b��c��ֵ��
��2������B����B��E��x����E��BB����OC���ڵ�F����ƽ����y���ֱ���ϸ����������ͬ��֪��C�ĺ�����Ϊ2����x=2����ֱ��y=��2x�Ľ���ʽ����õ�C����...
��1������2����A/������Ϊ����3,4������A/�ڸ��������ϣ���3����P�˶���ʱ���ı���PACM��ƽ���ı��Σ�
�������������������1������A��B��������������ߵĽ���ʽ���õ�����b��c�Ķ�Ԫһ�η����飬�Ӷ��ɽ��b��c��ֵ��
��2������B����B��E��x����E��BB����OC���ڵ�F����ƽ����y���ֱ���ϸ����������ͬ��֪��C�ĺ�����Ϊ2����x=2����ֱ��y=��2x�Ľ���ʽ����õ�C����...
��ͼ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����E��F�ֱ���OA��OC��
��1������������������OB=OD���ڡ�1=��2����OE=OF���������ѡȡ��������֤����BEO�ա�DFO��
��2���ڣ�1������������ѡ������ǰ���£�����AE=CF����֤���ı���ABCD��ƽ���ı��Σ�
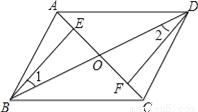
 ��1������������2��������.
�������������������1��ѡȡ�٢ڣ�����ASA�ж���BEO�ա�DFO��Ҳ��ѡȡ�ڢۣ�����AAS�ж���BEO�ա�DFO������ѡȡ�٢ۣ�����SAS�ж���BEO�ա�DFO��
��2�����ݡ�BEO�ա�DFO�ɵ�EO��FO��BO��DO���ٸ��ݵ�ʽ�����ʿɵ�AO��CO�����������Խ�����ƽ�ֵ��ı�����ƽ���ı��οɵý��ۣ�
���������
֤������1��ѡȡ�٢ڣ�
...
��1������������2��������.
�������������������1��ѡȡ�٢ڣ�����ASA�ж���BEO�ա�DFO��Ҳ��ѡȡ�ڢۣ�����AAS�ж���BEO�ա�DFO������ѡȡ�٢ۣ�����SAS�ж���BEO�ա�DFO��
��2�����ݡ�BEO�ա�DFO�ɵ�EO��FO��BO��DO���ٸ��ݵ�ʽ�����ʿɵ�AO��CO�����������Խ�����ƽ�ֵ��ı�����ƽ���ı��οɵý��ۣ�
���������
֤������1��ѡȡ�٢ڣ�
... ��ͼ��ƽ���ı���ABCD���ܳ���26cm���Խ���AC��BD���ڵ�O��AC��AB��E��BC�е㣬��AOD���ܳ��ȡ�AOB���ܳ���3cm����AE�ij���Ϊ��������
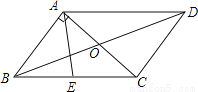
A. 3cm B. 4cm C. 5cm D. 8cm
 B
�������������������?ABCD���ܳ�Ϊ26cm��
��AB+AD=13cm��OB=OD��
�ߡ�AOD���ܳ��ȡ�AOB���ܳ���3cm��
�ࣨOA+OD+AD��-��OA+OB+AB��=AD-AB=3cm��
��AB=5cm��AD=8cm��
��BC=AD=8cm��
��AC��AB��E��BC�е㣬
��AE=BC=4cm.
��ѡB��
B
�������������������?ABCD���ܳ�Ϊ26cm��
��AB+AD=13cm��OB=OD��
�ߡ�AOD���ܳ��ȡ�AOB���ܳ���3cm��
�ࣨOA+OD+AD��-��OA+OB+AB��=AD-AB=3cm��
��AB=5cm��AD=8cm��
��BC=AD=8cm��
��AC��AB��E��BC�е㣬
��AE=BC=4cm.
��ѡB�� ���κ���y��ax2��bx��c��ͼ����ͼ11��ʾ����P��|2a��b|��|3b��2c|��Q��|2a��b|��|3b��2c|����P��Q�Ĵ�С��ϵ��______��
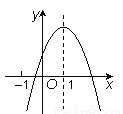
 P��Q
���������������ߵĿ������£�
��a��0��
��
��b��0��
��2a-b��0��
��
��b+2a=0��
x=-1ʱ��y=a-b+c��0��
��
��3b-2c��0��
����������y����������ཻ��
��c��0��
��3b+2c��0��
��P=3b-2c��
Q=b-2a-3b-2c=-2a-2b-2c��
��Q-P=-2a-2b-2c-3b+2c=-2a-5b=-...
P��Q
���������������ߵĿ������£�
��a��0��
��
��b��0��
��2a-b��0��
��
��b+2a=0��
x=-1ʱ��y=a-b+c��0��
��
��3b-2c��0��
����������y����������ཻ��
��c��0��
��3b+2c��0��
��P=3b-2c��
Q=b-2a-3b-2c=-2a-2b-2c��
��Q-P=-2a-2b-2c-3b+2c=-2a-5b=-... �ڶ��κ���y=ax2+bx+c�У����a��0��b��0��c��0����ô����ͼ��һ����������������
A. ��һ���� B. �ڶ����� C. �������� D. ��������
 C
����������������
�١�a��0��c��0����������߿��ڷ������ϣ�����y�ύ�������
�ڡ�a��0��b��0������κ���y=ax2+bx+c�ĺ���ͼ��ĶԳ�����x=����0������κ���y=ax2+bx+c�ĺ���ͼ��ĶԳ����ڵ�һ���ޣ�
�ۺϢ٢ڣ����κ���y=ax2+bx+c��ͼ��һ���������������ޣ�
��ѡC��
C
����������������
�١�a��0��c��0����������߿��ڷ������ϣ�����y�ύ�������
�ڡ�a��0��b��0������κ���y=ax2+bx+c�ĺ���ͼ��ĶԳ�����x=����0������κ���y=ax2+bx+c�ĺ���ͼ��ĶԳ����ڵ�һ���ޣ�
�ۺϢ٢ڣ����κ���y=ax2+bx+c��ͼ��һ���������������ޣ�
��ѡC�� ��ͼ��������С����Ǧ���¼����м�������������Ǧ���н��߶�y(m)��ˮƽ����x(m)֮��Ĺ�ϵΪy���� (x��4)2��3���ɴ˿�֪Ǧ���Ƴ��ľ�����___________.
(x��4)2��3���ɴ˿�֪Ǧ���Ƴ��ľ�����___________.

 10
����������������
���У���y=0���ã���ã�x1=10��x2=��2����ȥ������Ǧ���Ƴ��ľ�����10m���ʴ�Ϊ��10��
10
����������������
���У���y=0���ã���ã�x1=10��x2=��2����ȥ������Ǧ���Ƴ��ľ�����10m���ʴ�Ϊ��10�� ��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ������˵��������ǣ� ��
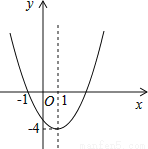
A��ͼ�����ֱ��x=1�Գ�
B������y=ax2+bx+c��a��0������Сֵ�ǩ�4
C����1��3�Ƿ���ax2+bx+c=0��a��0����������
D����x��1ʱ��y��x�����������
 D
��������
������������ݶԳ��ἰ��������x�ύ���������϶��κ��������ʣ����ɶ����ý��۽����жϣ�
��������
A���۲�ͼ��֪�����ߵĶԳ���Ϊֱ��x=1����ͼ�����ֱ��x=1�Գƣ���ȷ���ʱ�ѡ��������⣻
B���۲�ͼ��֪�����ߵĶ�������Ϊ��1����4�����������߿������ϣ����Ժ���y=ax2+bx+c��a��0������Сֵ�ǩ�4����ȷ���ʱ�ѡ��������⣻
C��...
D
��������
������������ݶԳ��ἰ��������x�ύ���������϶��κ��������ʣ����ɶ����ý��۽����жϣ�
��������
A���۲�ͼ��֪�����ߵĶԳ���Ϊֱ��x=1����ͼ�����ֱ��x=1�Գƣ���ȷ���ʱ�ѡ��������⣻
B���۲�ͼ��֪�����ߵĶ�������Ϊ��1����4�����������߿������ϣ����Ժ���y=ax2+bx+c��a��0������Сֵ�ǩ�4����ȷ���ʱ�ѡ��������⣻
C��... ����һö����Ӳ�ң���غ����泯�ϡ���һ�¼��ǣ�������
A. ��Ȼ�¼� B. ����¼� C. ȷ���¼� D. �������¼�
 B
����������������¼��Ķ��壬����¼����ǿ��ܷ�����Ҳ���ܲ��������¼��������жϣ�
��1ö����Ӳ�ң���غ�������泯�ϣ�Ҳ���ܷ��泯�ϣ�����1ö����Ӳ�ң���غ����泯��������¼�.
��ѡB.
B
����������������¼��Ķ��壬����¼����ǿ��ܷ�����Ҳ���ܲ��������¼��������жϣ�
��1ö����Ӳ�ң���غ�������泯�ϣ�Ҳ���ܷ��泯�ϣ�����1ö����Ӳ�ң���غ����泯��������¼�.
��ѡB. һ��ͼ�����۾���ƽ�Ʊ任�����Ǿ�����ת�任������˵����ȷ���ǣ�������
�ٶ�Ӧ�߶�ƽ��
�ڶ�Ӧ�߶����
��ͼ�ε���״�ʹ�С��û�з����仯
�ܶ�Ӧ����ȣ�
A. �٢ڢ� B. �ڢۢ� C. �٢ڢ� D. �٢ۢ�
 B
����������������
��ƽ�ƺ��Ӧ�߶�ƽ�У���ת��Ӧ�߶β�һ��ƽ�У��ʱ�С�����
������ƽ�ƻ�����ת����Ӧ�߶���ȣ��ʱ�С����ȷ��
������ƽ�ƻ�����ת��ͼ�ε���״�ʹ�С��û�з����仯���ʱ�С����ȷ��
������ƽ�ƻ�����ת����Ӧ����ȣ��ʱ�С����ȷ��
����������˵����ȷ���Ǣڢۢܣ�
��ѡB��
B
����������������
��ƽ�ƺ��Ӧ�߶�ƽ�У���ת��Ӧ�߶β�һ��ƽ�У��ʱ�С�����
������ƽ�ƻ�����ת����Ӧ�߶���ȣ��ʱ�С����ȷ��
������ƽ�ƻ�����ת��ͼ�ε���״�ʹ�С��û�з����仯���ʱ�С����ȷ��
������ƽ�ƻ�����ת����Ӧ����ȣ��ʱ�С����ȷ��
����������˵����ȷ���Ǣڢۢܣ�
��ѡB�� 
