在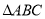 中,
中, 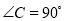 ,
, 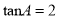 ,则
,则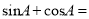 _______ .
_______ .
 【解析】试题解析:如图,
∵tanA=2,
∴设AB=x,则BC=2x,
AC= ,
则有:sinA+cosA=.
故答案为: .
【解析】试题解析:如图,
∵tanA=2,
∴设AB=x,则BC=2x,
AC= ,
则有:sinA+cosA=.
故答案为: . 在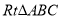 中,
中, 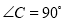 ,
, 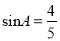 ,
, 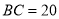 ,则
,则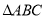 的面积为________.
的面积为________.
 150
【解析】试题解析:∵在Rt△ABC中,∠C=90°,sinA=,
∴AB=,
∴AC=,
则△ABC的面积为: AC•BC=×15×20=150.
故答案为:150.
150
【解析】试题解析:∵在Rt△ABC中,∠C=90°,sinA=,
∴AB=,
∴AC=,
则△ABC的面积为: AC•BC=×15×20=150.
故答案为:150. 在等腰直角三角形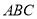 中,
中, 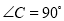 ,
, 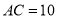 ,
, 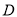 是
是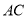 上一点,若
上一点,若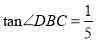 ,求
,求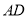 的长.
的长.
 AD=8
【解析】试题分析:利用等腰直角三角形的性质得BC=AC=10,再在Rt△BCD中,利用正切的定义得到tan∠DBC=,则可计算出CD=2,然后计算AC-CD即可.
试题解析:如图,
∵△ABC为等腰直角三角形,
∴BC=AC=10,
在Rt△BCD中,∵tan∠DBC=,
∴CD=×10=2,
∴AD=AC-CD=10-2=8.
AD=8
【解析】试题分析:利用等腰直角三角形的性质得BC=AC=10,再在Rt△BCD中,利用正切的定义得到tan∠DBC=,则可计算出CD=2,然后计算AC-CD即可.
试题解析:如图,
∵△ABC为等腰直角三角形,
∴BC=AC=10,
在Rt△BCD中,∵tan∠DBC=,
∴CD=×10=2,
∴AD=AC-CD=10-2=8. 如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为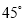 ,如果梯子的底端
,如果梯子的底端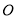 固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为
固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为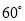 ,求此保管室的宽度
,求此保管室的宽度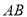 的长.
的长.
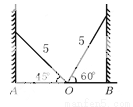
 【解析】由于两边的墙都和地面垂直,所以构成了两个直角三角形.
∵cos45°==,∴;而cos60°==,∴BO=.
∴AB=AO+BO==.
【解析】由于两边的墙都和地面垂直,所以构成了两个直角三角形.
∵cos45°==,∴;而cos60°==,∴BO=.
∴AB=AO+BO==. 如图所示,一测量员站在岸边的A处,刚好正对河岸另一边B处的一棵大树,这位测量员沿河岸向右走了50 m到达C处,在C处测得∠ACB=38°,求河的宽度.(精确到0.01 m,tan 38°≈0.7813)
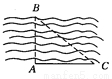
 39.07
【解析】试题分析:在直角三角形中,根据已知条件利用所给角的正切值求得AB即可.
试题解析:在Rt△BAC中,∠ACB=38°.
则AB=AC•tan38°≈50×0.7813=39.065≈39.07(米).
答:河的宽度约为39.07米.
39.07
【解析】试题分析:在直角三角形中,根据已知条件利用所给角的正切值求得AB即可.
试题解析:在Rt△BAC中,∠ACB=38°.
则AB=AC•tan38°≈50×0.7813=39.065≈39.07(米).
答:河的宽度约为39.07米. 如图所示,两建筑物的水平距离为24 m,从A点测得D点的俯角为60°,测得C点的仰角为40°,求这两座建筑物的高.(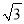 ≈1.732,tan 40°≈0.8391,精确到0.01 m)
≈1.732,tan 40°≈0.8391,精确到0.01 m)
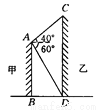
 61.7l m
【解析】试题分析:过点A作AE⊥CD于点E,可得四边形ABDE为矩形,AB=ED,BD=AE,然后在Rt△AED和Rt△AEC中,分别求出DE和EC的长度,继而可求得建筑物CD的高度和建筑物AB的高度.
试题解析:作AE⊥CD于E,
则AE=BD=24m,
在Rt△AED中,tan∠DAE=,
∴DE=AEtan 60°≈24×1.732≈41.57(...
61.7l m
【解析】试题分析:过点A作AE⊥CD于点E,可得四边形ABDE为矩形,AB=ED,BD=AE,然后在Rt△AED和Rt△AEC中,分别求出DE和EC的长度,继而可求得建筑物CD的高度和建筑物AB的高度.
试题解析:作AE⊥CD于E,
则AE=BD=24m,
在Rt△AED中,tan∠DAE=,
∴DE=AEtan 60°≈24×1.732≈41.57(... 如图所示,一个能张开54°的圆规,若两脚长均为15 cm,则该圆规所画的圆中最大的直径是多少?(sin 27°≈0.4540,精确到0.01 cm)
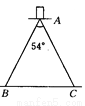
 27.24cm
【解析】试题分析:作AD⊥BC于D,根据等腰三角形的性质求出BD的长,即可求出BC的长.
试题解析:作AD⊥BC于D,则∠BAD=27°,
∴BD=ABsin 27°=15×sin 27°≈15×0.4540=6.81(cm),∴BC=2BD≈2×6.81=13.62(cm),∴直径=2BC≈2×13.62=27.24(cm).即该圆规所画的圆中最大的直径约是27...
27.24cm
【解析】试题分析:作AD⊥BC于D,根据等腰三角形的性质求出BD的长,即可求出BC的长.
试题解析:作AD⊥BC于D,则∠BAD=27°,
∴BD=ABsin 27°=15×sin 27°≈15×0.4540=6.81(cm),∴BC=2BD≈2×6.81=13.62(cm),∴直径=2BC≈2×13.62=27.24(cm).即该圆规所画的圆中最大的直径约是27... 如图所示的是一辆自行车的侧面示意图.已知车轮直径为65 cm,车架中AC的长为42 cm,座杆AE的长为18 cm,点E,A,C在同一条直线上,后轴轴心B与中轴轴心C所在直线BC与地面平行,∠C=73°,求车座E到地面的距离EF.(结果精确到l cm,参考数据:sin 73°≈0.96,cos 73°≈0.29,tan 73°≈3.27)
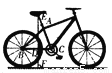
 90
【解析】试题分析:如图所示,题中所求线段是EF,而DF=0.5×65=32.5为已知,所以只需求出ED,而ED在直角三角形ECD中,且∠C=73°为已知,斜边EC=60为已知,所以可用正弦的概念求出ED=60×sin73°≈60×0.96≈57.6,再加上32.5即EF的长约为90cm.
试题解析:如图,在Rt△EDC中,
CE=AE+AC=18+42=60(cm).
...
90
【解析】试题分析:如图所示,题中所求线段是EF,而DF=0.5×65=32.5为已知,所以只需求出ED,而ED在直角三角形ECD中,且∠C=73°为已知,斜边EC=60为已知,所以可用正弦的概念求出ED=60×sin73°≈60×0.96≈57.6,再加上32.5即EF的长约为90cm.
试题解析:如图,在Rt△EDC中,
CE=AE+AC=18+42=60(cm).
... 用直尺和圆规作一个角的平分线如图所示,说明∠AOC=∠BOC的依据是( ).
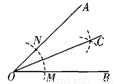
A. SSS B. ASA C. AAS D. 角平分线上的点到角两边距离相等
 A
【解析】试题分析:连接NC,MC,根据SSS证△ONC≌△OMC,即可推出答案.
连接NC,MC,在△ONC和△OMC中,
∴△ONC≌△OMC(SSS), ∴∠AOC=∠BOC
A
【解析】试题分析:连接NC,MC,根据SSS证△ONC≌△OMC,即可推出答案.
连接NC,MC,在△ONC和△OMC中,
∴△ONC≌△OMC(SSS), ∴∠AOC=∠BOC 作∠AOB的平分线时,以O为圆心,某一长度为半径作弧,与OA,OB分别相交于点C,D,然后分别以点C,D为圆心,适当的长度为半径作弧,使两弧相交于一点,则这个适当的长度为( )
A. 大于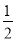 CD B. 等于
CD B. 等于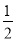 CD
CD
C. 小于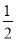 CD D. 以上答案都不对
CD D. 以上答案都不对
 A
【解析】要保证所作的是角平分线,根据全等三角形的性质,则应再保证两弧相交的点到点C、D的距离相等;画弧时,两弧应有交点才能构成三角形,据此结合三角形的三边关系分析即可.
【解析】
根据三角形两边之和大于第三边的性质可知,
画的时候,为了让两条弧有交点,必须是以大于CD的长为半径画弧.
故选A.
A
【解析】要保证所作的是角平分线,根据全等三角形的性质,则应再保证两弧相交的点到点C、D的距离相等;画弧时,两弧应有交点才能构成三角形,据此结合三角形的三边关系分析即可.
【解析】
根据三角形两边之和大于第三边的性质可知,
画的时候,为了让两条弧有交点,必须是以大于CD的长为半径画弧.
故选A.