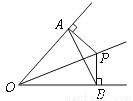
根据图中尺规作图的痕迹,先判断得出结论:__________,并说明理由.
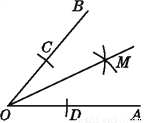
OM平分∠BOA
【解析】根据全等三角形的判定及性质即可得出结论.
【解析】
如图所示,连接CM,DM,
由作图的痕迹可知,OC=OD,CM=DM.
又因为OM=OM,
所以△COM≌△DOM.
所以∠COM=∠DOM.
所以OM平分∠BOA.
故答案为：OM平分∠BOA. 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
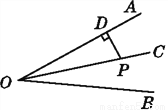
A. 6 B. 5 C. 4 D. 3
A
【解析】试题分析：如图，过点P作PE⊥OB于点E，∵OC是∠AOB的平分线，PD⊥OA于D，∴PE=PD，∵PD=6，∴PE=6，即点P到OB的距离是6．故选A． 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是（ ）
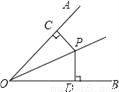
A. PC=PD B. ∠CPD=∠DOP C. ∠CPO=∠DPO D. OC=OD
B
【解析】试题分析：已知OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C、D，根据角平分线的性质可得PC=PD，A正确；在Rt△OCP与Rt△ODP中，OP=OP,PC=PD，由HL可判定△OCP≌△ODP，根据全等三角形的性质可得∠CPO=∠DPO，OC=OD，故C、D正确．不能得出∠CPD=∠DOP，故B错误．故答案选B． 如图，OP平分∠AOB，PA⊥OA,PB⊥OB，垂足分别为A，B。下列结论中不一定成立的是（ ）
A、PA=PB B、PO平分∠AOB
C、OA=OB D、AB垂直平分OP
D
【解析】
试题分析：本题要从已知条件OP平分∠AOB入手，利用角平分线的性质：因OP平分∠AOB，PA⊥OA，PB⊥OB，得到PA=PB，进而推出△AOE≌△BOE，从未得到∠APO=∠BPO，OA=OB，因此A、B、C项正确；设PO与AB相交于E，由OA=OB，∠AOP=∠BOP，OE=OE，得证△AOE≌△BOE，进而得∠AEO=∠BEO=90°，因此得证OP垂直AB，而不能得... 如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD＝8，则点P到BC的距离是（ ）
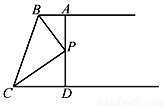
A. 8 B. 6 C. 4 D. 2
C
【解析】过点P作PE⊥BC于E，
∵AB∥CD，PA⊥AB，
∴PD⊥CD，
∵BP和CP分别平分∠ABC和∠DCB，
∴PA=PE，PD=PE，
∴PE=PA=PD，
∵PA+PD=AD=8，
∴PA=PD=4，
∴PE=4．
故选C． 如图，已知在△ABC中，CD是AB边上的高，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于_____．
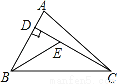
5
【解析】试题解析：
作EF⊥BC于F，
∵BE平分∠ABC，EF⊥BC，ED⊥AB，
∴EF=DE=2，
∴△BCE的面积
故答案为：5. 如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
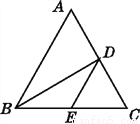
A. AD>DE B. AD=DE
C. AD<DE D. 不确定
D
【解析】根据角平分线上的点到角的两边距离相等可得点D到AB、BC的距离相等，AD、BE都不是点D到AB、BC的距离，大小不确定．
【解析】
∵BD平分∠ABC，
∴点D到AB、BC的距离相等，
∵AD不是点D到AB的距离，点E是BC上一点，
∴AD、DE的大小不确定.
故选D. 如图，一块余料ABCD，AD∥BC，现进行如下操作：以点B为圆心，适当长为半径画弧，分别交BA，BC于点G，H；再分别以点G，H为圆心，大于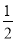
GH的长为半径画弧，两弧在∠ABC内部相交于点O，画射线BO，交AD于点E．
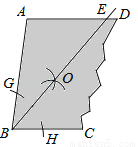
（1）求证：AB=AE；
（2）若∠A=100°，求∠EBC的度数．
（1）证明见试题解析；（2）40°．
【解析】试题分析：（1）由角平分线的性质，可以得到∠AEB=∠EBC，由角平分线的性质，得到∠EBC=∠ABE，由等腰三角形的判定，可得答案；
（2）由三角形的内角和定理，可得∠AEB，由平行线的性质，可得答案．
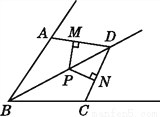
试题解析：（1）∵AD∥BC，∴∠AEB=∠EBC，∵ BE是∠ABC的角平分线，∴∠EBC=∠ABE，∴∠AEB=∠ABE，∴A... 如图,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于点M,PN⊥CD于点N.
试说明:PM=PN.
见解析
【解析】根据角平分线的性质以及已知条件证得△ABD≌△CBD（SAS），然后由全等三角形的对应角相等推知∠ADB=∠CDB；再根据角平分线的判定定理即可得出结论．
证明：因为BD为∠ABC的平分线,
所以∠ABD=∠CBD.
又因为BA=BC,BD=BD,
所以△ABD≌△CBD(SAS).
所以∠ADB=∠CDB.
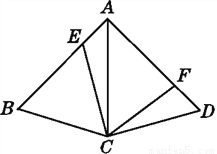
因为点P在BD上,PM⊥AD,... 如图,在四边形ABCD中,AC为∠BAD的平分线,AB=AD,点E,F分别在AB,AD上,且AE=DF,请说明为何四边形AECF的面积为四边形ABCD的一半.
见解析
【解析】先作CG⊥AB于G,CH⊥AD于H,利用角平分线的性质得出CG=CH，再利用面积间的等量代换即可推出结论.
证明：如图,作CG⊥AB于G,CH⊥AD于H,
因为AC为∠BAD的平分线,
所以CG=CH.
因为AB=AD,
所以S△ABC=S△ACD.
又因为AE=DF,
所以S△AEC=S△CDF.
因为S△BCE=S△ABC-...