题目内容
如图,在四边形ABCD中,AC为∠BAD的平分线,AB=AD,点E,F分别在AB,AD上,且AE=DF,请说明为何四边形AECF的面积为四边形ABCD的一半.
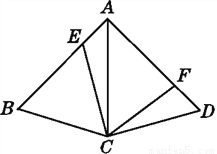
 见解析
【解析】先作CG⊥AB于G,CH⊥AD于H,利用角平分线的性质得出CG=CH,再利用面积间的等量代换即可推出结论.
证明:如图,作CG⊥AB于G,CH⊥AD于H,
因为AC为∠BAD的平分线,
所以CG=CH.
因为AB=AD,
所以S△ABC=S△ACD.
又因为AE=DF,
所以S△AEC=S△CDF.
因为S△BCE=S△ABC-...
见解析
【解析】先作CG⊥AB于G,CH⊥AD于H,利用角平分线的性质得出CG=CH,再利用面积间的等量代换即可推出结论.
证明:如图,作CG⊥AB于G,CH⊥AD于H,
因为AC为∠BAD的平分线,
所以CG=CH.
因为AB=AD,
所以S△ABC=S△ACD.
又因为AE=DF,
所以S△AEC=S△CDF.
因为S△BCE=S△ABC-...
 快乐5加2金卷系列答案
快乐5加2金卷系列答案下列分式是最简分式的是( )
A. 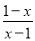 B.
B. 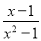
C. 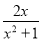 D.
D. 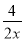
 C
【解析】根据最简分式的特点,分子分母没有公因式,因此A可化为,不是最简分式;B可化为,不是最简分式;C是最简分式;D可化简为,不是最简分式.
故选:C.
C
【解析】根据最简分式的特点,分子分母没有公因式,因此A可化为,不是最简分式;B可化为,不是最简分式;C是最简分式;D可化简为,不是最简分式.
故选:C. 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB= .
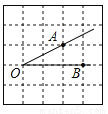
 .
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: .
.
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: . 某移动通信公司开设了两种通信业务,“全球通”:使用时首先缴50元月租费,然后每通话1分钟,付话费0.4元;“动感地带”:不缴月租费,每通话1分钟,付话费0.6元(本题的通话均指市内通话).若一个月通话x分钟,两种方式的费用分别为y1元和y2元.
(1)写出y1,y2与x之间的关系式;
(2)一个月内通话多少分钟,两种方式费用相同?
(3)某人估计一个月内通话300分钟,应选择哪种方式更合算些?
 【解析】
(1)y1=50+0.4x,y2=0.6x (2)当每个月通话250分钟时,两种方式费用相同 (3)使用“全球通”合算
【解析】试题分析:(1)理解每种通信业务的付费方式,依据每分钟通话费用×通话时长便可确定每种方式的费用,进而写出y1、y2的关系式;
对于(2),令y1=y2,解方程即可;
对于(3),令x=300,分别求出y1、y2的值,再做比较即可.
【解...
【解析】
(1)y1=50+0.4x,y2=0.6x (2)当每个月通话250分钟时,两种方式费用相同 (3)使用“全球通”合算
【解析】试题分析:(1)理解每种通信业务的付费方式,依据每分钟通话费用×通话时长便可确定每种方式的费用,进而写出y1、y2的关系式;
对于(2),令y1=y2,解方程即可;
对于(3),令x=300,分别求出y1、y2的值,再做比较即可.
【解... 甲、乙两人沿相同的路线从A到B匀速行驶,A,B两地间的路程为20 km,他们行进的路程s(km)与甲、乙出发的时间t(h)之间关系的图象如图所示,根据图象信息,下列说法正确的是( )
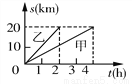
A. 甲的速度是4 km/h B. 乙的速度是10 km/h C. 乙比甲晚出发1 h D. 甲比乙晚到B地3 h
 B
【解析】A. 甲的速度是20÷4=5 km/h,故不正确;
B. 乙的速度是20÷2=10 km/h,故正确;
C. 由图像知,乙和甲同时出发,故不正确;
D. 由图像知,甲比乙晚到B地2 h,故不正确;
故选B.
B
【解析】A. 甲的速度是20÷4=5 km/h,故不正确;
B. 乙的速度是20÷2=10 km/h,故正确;
C. 由图像知,乙和甲同时出发,故不正确;
D. 由图像知,甲比乙晚到B地2 h,故不正确;
故选B. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
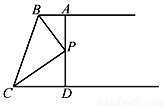
A. 8 B. 6 C. 4 D. 2
 C
【解析】过点P作PE⊥BC于E,
∵AB∥CD,PA⊥AB,
∴PD⊥CD,
∵BP和CP分别平分∠ABC和∠DCB,
∴PA=PE,PD=PE,
∴PE=PA=PD,
∵PA+PD=AD=8,
∴PA=PD=4,
∴PE=4.
故选C.
C
【解析】过点P作PE⊥BC于E,
∵AB∥CD,PA⊥AB,
∴PD⊥CD,
∵BP和CP分别平分∠ABC和∠DCB,
∴PA=PE,PD=PE,
∴PE=PA=PD,
∵PA+PD=AD=8,
∴PA=PD=4,
∴PE=4.
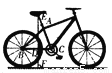
故选C. 如图所示的是一辆自行车的侧面示意图.已知车轮直径为65 cm,车架中AC的长为42 cm,座杆AE的长为18 cm,点E,A,C在同一条直线上,后轴轴心B与中轴轴心C所在直线BC与地面平行,∠C=73°,求车座E到地面的距离EF.(结果精确到l cm,参考数据:sin 73°≈0.96,cos 73°≈0.29,tan 73°≈3.27)
 90
【解析】试题分析:如图所示,题中所求线段是EF,而DF=0.5×65=32.5为已知,所以只需求出ED,而ED在直角三角形ECD中,且∠C=73°为已知,斜边EC=60为已知,所以可用正弦的概念求出ED=60×sin73°≈60×0.96≈57.6,再加上32.5即EF的长约为90cm.
试题解析:如图,在Rt△EDC中,
CE=AE+AC=18+42=60(cm).
...
90
【解析】试题分析:如图所示,题中所求线段是EF,而DF=0.5×65=32.5为已知,所以只需求出ED,而ED在直角三角形ECD中,且∠C=73°为已知,斜边EC=60为已知,所以可用正弦的概念求出ED=60×sin73°≈60×0.96≈57.6,再加上32.5即EF的长约为90cm.
试题解析:如图,在Rt△EDC中,
CE=AE+AC=18+42=60(cm).
... 在△ABC中,AB=AC,且BC=8cm,BD是腰AC的中线,△ABC的周长分为两部分,已知它们的差为2cm,则等腰三角形的腰长为__________.
 10cm或6cm
【解析】如图∵BD是腰AC的中线,
∴AD=CD,
①当△ABD的周长与△BCD的周长差为2时,即AB+AD+BD-(BD+BC+CD)=2,
∴AB-BC=2,
∵BC=8cm,
∴AB=10cm.
②当△BCD的周长与△ABD的周长差为2时,即BD+BC+CD -(AB+AD+BD)=2,
∴BC - AB =2,
∵BC...
10cm或6cm
【解析】如图∵BD是腰AC的中线,
∴AD=CD,
①当△ABD的周长与△BCD的周长差为2时,即AB+AD+BD-(BD+BC+CD)=2,
∴AB-BC=2,
∵BC=8cm,
∴AB=10cm.
②当△BCD的周长与△ABD的周长差为2时,即BD+BC+CD -(AB+AD+BD)=2,
∴BC - AB =2,
∵BC... 小明家里的阳台地面,水平铺设着仅黑白颜色不同的18块方砖(如图),他从房间里向阳台抛小皮球,小皮球最终随机停留在某块方砖上.
(1)求小皮球分别停留在黑色方砖与白色方砖上的概率.
(2)(1)中哪个概率较大?要使这两个概率相等,应改变哪块方砖的颜色?

 (1), (2)小皮球停留在黑色方砖上的概率大.
【解析】试题分析:(1)根据小球停在黑色方砖上的概率就是黑色方砖面积与总面积的比值,小球停在白色方砖上的概率就是白色方砖面积与总面积的比值,再根据黑色方砖、白色方砖的个数与总个数之间的关系,即可求出答案;
(2)要想这两个概率相等,只要使黑色方砖的个数与白色方砖的个数相等即可.
试题解析:【解析】
(1)∵白色方砖8块,黑色方砖...
(1), (2)小皮球停留在黑色方砖上的概率大.
【解析】试题分析:(1)根据小球停在黑色方砖上的概率就是黑色方砖面积与总面积的比值,小球停在白色方砖上的概率就是白色方砖面积与总面积的比值,再根据黑色方砖、白色方砖的个数与总个数之间的关系,即可求出答案;
(2)要想这两个概率相等,只要使黑色方砖的个数与白色方砖的个数相等即可.
试题解析:【解析】
(1)∵白色方砖8块,黑色方砖... 
