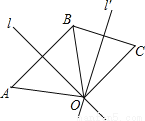
如图，l是线段AB的对称轴，l′是线段BC的对称轴，l和l′相交于点O．OA与OC相等吗？为什么？
相等，理由见解析
【解析】试题分析：由轴对称的性质即可证明．
试题解析：【解析】
∵l是线段AB的对称轴，∴OA=OB，
∵l′是线段BC的对称轴，∴OB=OC，
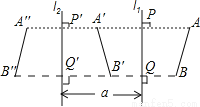
∴OA=OC． 设直线l1和直线l2平行，且l1和l2间的距离为a．如果线段AB在l1的右侧，并设AB关于l1的对称图形是A′B′，而A′B′关于l2的对称图形是A″B″（如图），那么，线段AB和A″B″有什么关系？
A''B''平行且等于AB，理由见解析
【解析】试题分析：根据轴对称的性质，及在平面内垂直于同一条直线的两条直线互相平行，即可判断ABB''A''为平行四边形，继而得出答案．
试题解析：【解析】
因为l1平行于l2，并且AA″垂直于l1，当然也垂直于l2，同理BB″也垂直于l1和l2．
又在平面内垂直于同一条直线的两条直线互相平行，
所以AA″∥BB″①
另一方面，... 两条直线相交，有_____对对顶角，三条直线两两相交，有_____对对顶角.
两 六
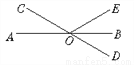
【解析】两条直线相交，有两对对顶角，三条直线两两相交，有六对对顶角. 如图，直线AB、CD相交于点O，OB平分∠DOE，若∠DOE=60°，则∠AOC的度数是_____.
30°
【解析】因为∠BOD=45°，所以∠AOC=∠BOD=45°（对顶角相等），因为OE⊥AB，∴∠AOE=90°，所以∠COE=∠COA+∠AOE=45°+90°=135°. 已知∠AOB=40°，OC平分∠AOB，则∠AOC的补角等于_____.
160°
【解析】
∵OC平分∠AOB，∠AOB=40°，
∴,
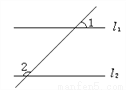
∴∠AOC的补角=180°-20°=160°. 如图，若l1∥l2，∠1=45°，则∠2=_____.
135
【解析】试题分析：根据对顶角的性质求出∠1的对顶角，然后根据两直线平行同旁内角互补得出∠2的度数. 如图，已知直线a∥b,c∥d，∠1=115°，则∠2=_____，∠3=_____.
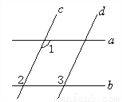
115° 115°
【解析】∵a∥b,∠1=115°，
∴∠2=∠1=115°.
∵c∥d，
∴∠3=∠2=115°. 一个角的余角比这个角的补角小_____.
90°
【解析】设这个角是x°，由题意得
（180°- x°）-（90°- x°）=90°. 如图，已知直线AB、CD、EF相交于点O，∠1=95°，∠2=32°，则∠BOE=_____.
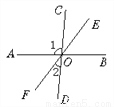
53°
【解析】由∠BOE与∠AOF是对顶角，可得∠BOE=∠AOF，又因为∠COD是平角，可得∠1+∠2+∠AOF=180°，将∠1=95°，∠2=32°代入，即可求得∠AOF的度数，即∠BOE的度数． 如图，∠1=82°，∠2=98°，∠3=80°,则∠4的度数为_____.
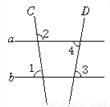
80°
【解析】
∵∠2=98°，
∴∠5=98°.
∵∠1=82°，
∴∠1+∠5=82°+98°=180°，
∴a∥b,
∵∠3=80°,
∴∠4=∠3=80°.