题目内容
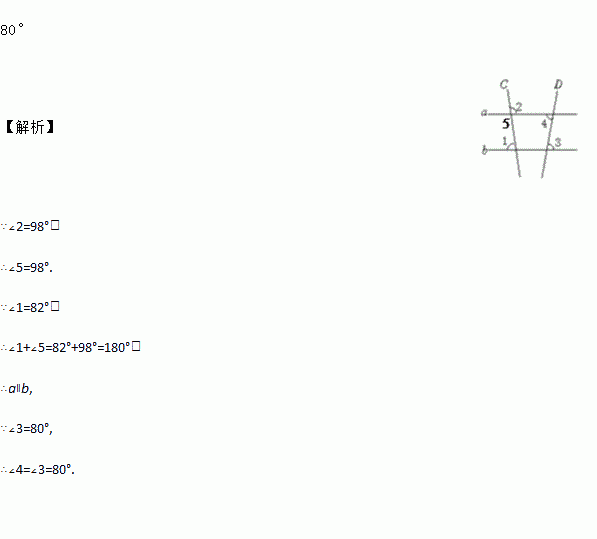
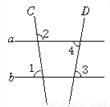
如图，∠1=82°，∠2=98°，∠3=80°,则∠4的度数为_____.
80°
【解析】
∵∠2=98°，
∴∠5=98°.
∵∠1=82°，
∴∠1+∠5=82°+98°=180°，
∴a∥b,
∵∠3=80°,
∴∠4=∠3=80°.
练习册系列答案
相关题目
如图，四边形ABCD中，AC垂直平分BD，垂足为E，下列结论不一定成立的是（ ）
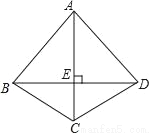
A. AB=AD B. AC平分∠BCD C. AB=BD D. △BEC≌△DEC
C
【解析】试题分析：根据AC垂直平分BD可得：△ABD为等腰三角形，即AB=AD，AC平分∠BAD，△BEC≌△DEC. 在Rt△ABC中，∠C＝90°，AB＝2BC，现给出下列结论：①sinA＝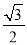
；②cosB＝
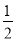；③tanA＝
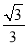；④tanB＝
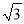，其中正确的结论是_____ .
②③④
【解析】∵在Rt△ABC中，∠C=90°，AB=2BC，∴。∴∠A=30°。∴∠B=60°。
∴cosB= cos60°=，tanA= tan300=，tanB= tan600=。
∴正确的结论是②③④。 如图，直线AB、CD相交于点O，EF⊥AB于O，且∠COE=50°，则∠BOD等于（ ）
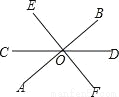
A. 40° B. 45° C. 55° D. 65°
A
【解析】∵EF⊥AB于O，∠COE=50°，
∴∠AOC=90°-50°=40°，
∵∠AOC与∠BOD是对顶角，
∴∠BOD=∠AOC=40°；
故选A。 如图，标有角号的7个角中共有________对内错角，________对同位角，________对同旁内角.
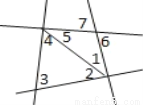
4对 2对 4对
【解析】【解析】
如图，共有4对内错角：分别是∠1和∠4，∠2和∠5，∠6和∠1，∠5和∠7；
2对同位角：分别是∠7和∠1，∠5和∠6；
4对同旁内角：分别是∠1和∠5、∠3和∠4、∠3和∠2、∠4和∠2． 已知∠AOB=40°，OC平分∠AOB，则∠AOC的补角等于_____.
160°
【解析】
∵OC平分∠AOB，∠AOB=40°，
∴,
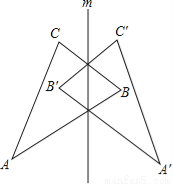
∴∠AOC的补角=180°-20°=160°. 如图，△ABC和△A′B′C′关于直线m对称．
（1）结合图形指出对称点．
（2）连接A、A′，直线m与线段AA′有什么关系？
（3）延长线段AC与A′C′，它们的交点与直线m有怎样的关系？其它对应线段（或其延长线）的交点呢？你发现了什么规律，请叙述出来与同伴交流．
【解析】
（1）对称点有A和A'，B和B'，C和C'．
（2）连接A、A′，直线m是线段AA′的垂直平分线．
（3）延长线段AC与A′C′，它们的交点在直线m上，其它对应线段（或其延长线）的交点也在直线m上，
即若两线段关于直线m对称，且不平行，则它们的交点或它们的延长线的交点在对称轴上．
【解析】本题考查轴对称图形的定义，如果一个图形沿着一条直线对折，两侧的图形能完全重... 已知x2-x-1=0,则代数式-x3+2x2+2 015的值为___________.
2016
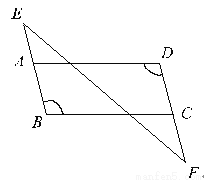
【解析】由已知得x2-x=1，所以-x3+2x2+2 015=-x(x2-x)+x2+2 015=-x+x2+2 015=2 016. 已知：如图，BE∥DF，∠B=∠D。求证：AD∥BC。
证明见解析
【解析】试题分析：根据BE∥DF得出∠D=∠EAD，结合已知条件得出∠B=∠EAD，从而根据同位角相等两直线平行得出答案．
试题解析：∵BE∥DF（已知），∴∠D=∠EAD（两条直线平行，内错角相等），
∵∠B=∠D（已知），∴∠B=∠EAD，∴AD∥BC（同位角相等，两直线平行）．