如图,下列说法错误的是( )
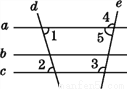
A. 若a∥b,b∥c,则a∥c B. 若∠1=∠2,则a∥c
C. 若∠3=∠2,则b∥c D. 若∠3+∠5=180°,则a∥c
C
【解析】试题分析：根据平行线的判定进行判断即可．
【解析】
A、若a∥b，b∥c，则a∥c，利用了平行公理，正确；
B、若∠1=∠2，则a∥c，利用了内错角相等，两直线平行，正确；
C、∠3=∠2，不能判断b∥c，错误；
D、若∠3+∠5=180°，则a∥c，利用同旁内角互补，两直线平行，正确；
故选C． 如图，点E在BC的延长线上，下列条件中能判定BC//AD的是 ( )
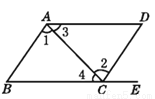
A. ∠1=∠2 B. ∠DAB+∠D=180° C. ∠3=∠4 D. ∠B=∠DCE
C
【解析】A. ∵∠1=∠2 ，∴AB∥CD, 故不正确；
B. ∵ ∠DAB+∠D=180° ，∴AB∥CD, 故不正确；
C. ∵∠3=∠4 ，∴ BC∥AD, 故正确；
D. ∵∠B=∠DCE，∴AB∥CD, 故不正确；
故选C. 如图,下列推理正确的有( )
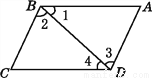
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠C=180°,所以BC∥AD.
A. 1个 B. 2个 C. 3个 D. 4个
A
【解析】（1）由∠1=∠2不能推导出BC∥AD，所以①中的推理错误；
（2）由∠2=∠3不能推导出AB∥CD，所以②中的推理错误；
（3）由∠BCD+∠ADC=180°能推导出BC∥AD，所以③中推理正确；
（4）由∠BCD+∠ABC=180°不能推导出BC∥AD，所以④中推理错误；
即4个推理中，只有③正确.
故选A. 如图,已知AB⊥BC,DC⊥BC,∠1=∠2,可得到BE∥CF,说明过程如下,请填上说明的依据:
因为AB⊥BC,DC⊥BC,
所以∠ABC=90°,
∠BCD=90°(______________),
所以∠ABC=∠BCD.
又因为∠1=∠2,
所以∠EBC=∠FCB.
所以BE∥CF(______________).
垂直的定义;内错角相等,两直线平行
【解析】试题分析：题中已知AB⊥BC，DC⊥BC，根据垂直的定义可得∠ABC=∠BCD=90°，又因为∠1=∠2，由等量减等量，差相等可得∠EBC=∠FCB，观察图形可知，∠EBC与∠FCB是直线BE与CF被直线BC所截的内错角，即可得证.
试题解析：因为AB⊥BC，DC⊥BC（已知），
所以∠ABC=∠BCD=90°（垂直的定义）.
又... 如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:
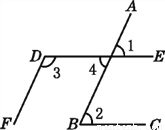
因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
DE;BC;同位角相等,两直线平行;对顶角相等;DF;AB;同旁内角互补,两直线平行
【解析】试题分析：由同位角相等，两直线平行可得DE∥BC，由对顶角相等可得∠4=65°，再由同旁内角互补，两直线平行可得DF∥AB.
试题解析：因为∠1=65°，∠2=65°，
所以∠1=∠2.
所以DE∥BC (同位角相等，两直线平行).
因为AB与DE相交，
所以∠1=∠... 如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
解:a与c平行.
理由:因为∠1=∠2( ),
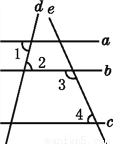
所以a∥b ( ).
因为∠3+∠4=180°( ),
所以b∥c ( ).
所以a∥c ( ).
已知;内错角相等,两直线平行;已知;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行
【解析】试题分析：根据平行线的性质得出a∥b，b∥c，即可推出答案．
试题解析：a∥c，
理由是：∵∠1=∠2(已知)，
∴a∥b(内错角相等，两直线平行)，
∵∠3+∠4=180°(已知)，
∴b∥c(同旁内角互补，两直线平行)，
∴a... 如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
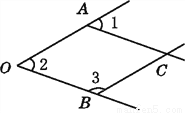
证明见解析.
【解析】试题分析：根据已知可得∠1=∠2，∠2+∠3=180°，由同位角相等，两直线平行即可得OB∥AC，由同旁内角互补，两直线平行可得OA∥BC．
试题解析：
OA∥BC，OB∥AC,理由如下：
∵∠1=50°，∠2=50°，
∴∠1=∠2，
∴OB∥AC，
∵∠2=50°，∠3=130°，
∴∠2+∠3=180°，
∴OA∥B... 如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.
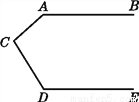
证明见解析.
【解析】试题分析：过点C作CF∥AB，结合已知可得∠A+∠ACF=180°，再根据已知角关系可得∠D+∠FCD=180°，根据平行线的判定即可得到CF∥DE，此时再次运用平行线的判定即可解答本题.
试题解析：过点C作CF∥AB.
∵CF∥AB，
∴∠A+∠ACF=180°.
∵∠A+∠ACD+∠D=360°，
∴∠D+∠FCD=180°，
∴... 下列各数中，负数是 （ ）
A. －(－5) B. －｜－5｜ C. (－5)2 D. －(－5)3．
B
【解析】A. －(－5)=5，是正数；
B. －｜－5｜=-5，是负数；
C. (－5)2 =25，是正数；
D. －(－5)3=-（-125）=125，是正数.
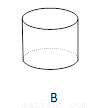
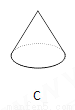
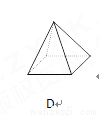
故选B. 下面立体图形，从正面、左面、上面观察都不可能看到长方形的是( )
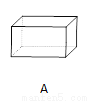
C
【解析】试题分析：A、主视图为长方形，左视图为长方形，俯视图为长方形，故本选项错误；
B、主视图为长方形，左视图为长方形，俯视图为圆，故本选项错误；
C、主视图为等腰三角形，左视图为等腰三角形，俯视图为圆，从正面、左面、上面观察都不可能看到长方形，故本选项正确；
D、主视图为三角形，左视图为三角形，俯视图为有对角线的矩形，故本选项错误．
故选：C．