题目内容
如图,点E在BC的延长线上,下列条件中能判定BC//AD的是 ( )
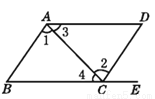
A. ∠1=∠2 B. ∠DAB+∠D=180° C. ∠3=∠4 D. ∠B=∠DCE
 C
【解析】A. ∵∠1=∠2 ,∴AB∥CD, 故不正确;
B. ∵ ∠DAB+∠D=180° ,∴AB∥CD, 故不正确;
C. ∵∠3=∠4 ,∴ BC∥AD, 故正确;
D. ∵∠B=∠DCE,∴AB∥CD, 故不正确;
故选C.
C
【解析】A. ∵∠1=∠2 ,∴AB∥CD, 故不正确;
B. ∵ ∠DAB+∠D=180° ,∴AB∥CD, 故不正确;
C. ∵∠3=∠4 ,∴ BC∥AD, 故正确;
D. ∵∠B=∠DCE,∴AB∥CD, 故不正确;
故选C.
练习册系列答案
相关题目
当x=2时,代数式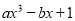 的值等于-9,那么当x=-1时,代数式 16ax-4bx3-2的值等于______.
的值等于-9,那么当x=-1时,代数式 16ax-4bx3-2的值等于______.
 18
【解析】把x=2代入=-9中,
得:8a-2b+1=-9
整理,得:4a-b=-5.
把x=-1代入16ax-4bx3-2中,
得:-16a+4b-2=-4(a-b)-2=-4×(-5)-2=18.
18
【解析】把x=2代入=-9中,
得:8a-2b+1=-9
整理,得:4a-b=-5.
把x=-1代入16ax-4bx3-2中,
得:-16a+4b-2=-4(a-b)-2=-4×(-5)-2=18. 下面的计算正确的是( )
A. 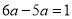 B.
B. 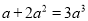 C.
C. 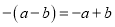 D.
D. 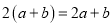
 C
【解析】A. ∵,故不正确;
B. ∵a与不是同类项,不能合并 ,故不正确;
C. ∵,故正确;
D. ∵,故不正确;
故选C.
C
【解析】A. ∵,故不正确;
B. ∵a与不是同类项,不能合并 ,故不正确;
C. ∵,故正确;
D. ∵,故不正确;
故选C. 如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
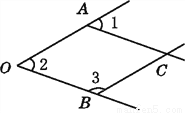
 证明见解析.
【解析】试题分析:根据已知可得∠1=∠2,∠2+∠3=180°,由同位角相等,两直线平行即可得OB∥AC,由同旁内角互补,两直线平行可得OA∥BC.
试题解析:
OA∥BC,OB∥AC,理由如下:
∵∠1=50°,∠2=50°,
∴∠1=∠2,
∴OB∥AC,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥B...
证明见解析.
【解析】试题分析:根据已知可得∠1=∠2,∠2+∠3=180°,由同位角相等,两直线平行即可得OB∥AC,由同旁内角互补,两直线平行可得OA∥BC.
试题解析:
OA∥BC,OB∥AC,理由如下:
∵∠1=50°,∠2=50°,
∴∠1=∠2,
∴OB∥AC,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥B... 下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. 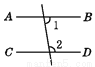 B.
B. 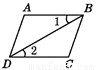 C.
C. 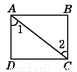 D.
D. 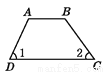
 B
【解析】试题分析:利用平行线的判定方法判断即可.
【解析】
如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选B
B
【解析】试题分析:利用平行线的判定方法判断即可.
【解析】
如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选B 如图,∠B=∠C,B、A、D三点在同一直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线.
求证:AE∥BC.
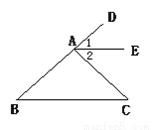
 见解析.
【解析】试题分析:先根据∠B=∠C,∠DAC=∠B+∠C得出∠DAC=2∠B,再由AE是∠DAC的平分线可知∠1=∠2,∠DAC=2∠1,故∠1=∠B,由此可得出结论.
试题解析:∵AE是∠DAC的平分线
∴∠DAC=2∠1
∵∠DAC=∠B+∠C,∠B=∠C
∴∠DAC=2∠B
∴∠1=∠B
∴AE∥BC
见解析.
【解析】试题分析:先根据∠B=∠C,∠DAC=∠B+∠C得出∠DAC=2∠B,再由AE是∠DAC的平分线可知∠1=∠2,∠DAC=2∠1,故∠1=∠B,由此可得出结论.
试题解析:∵AE是∠DAC的平分线
∴∠DAC=2∠1
∵∠DAC=∠B+∠C,∠B=∠C
∴∠DAC=2∠B
∴∠1=∠B
∴AE∥BC 如图,在△ABC中,∠C=40°,∠B=68°,AB、AC的垂直平分线分别交BC于D、E.求∠EAD的度数.
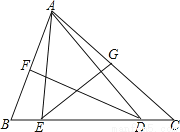
 36°
【解析】试题分析:根据三角形内角和定理求出∠BAC的度数,根据线段的垂直平分线的性质得到DA=DB,EA=EC,根据等腰三角形的性质分别求出∠DAC和∠BAE的度数,计算得到∠EAD的度数.
试题解析:∵∠C=40°,∠B=68°,
∴∠BAC=72°,
∵DF是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=68°,
∴∠DAC=4°,...
36°
【解析】试题分析:根据三角形内角和定理求出∠BAC的度数,根据线段的垂直平分线的性质得到DA=DB,EA=EC,根据等腰三角形的性质分别求出∠DAC和∠BAE的度数,计算得到∠EAD的度数.
试题解析:∵∠C=40°,∠B=68°,
∴∠BAC=72°,
∵DF是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=68°,
∴∠DAC=4°,... 如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确结论的个数是( )
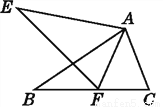
A. 1个 B. 2个 C. 3个 D. 4个
 C
【解析】根据全等三角形对应边相等,全等三角形对应角相等结合图象解答即可.
∵△ABC≌△AEF,
∴AC=AF,EF=BC,∠EAF=∠BAC,故(1)(3)正确,
∴∠EAF-∠BAF=∠BAC-∠BAF,
即∠EAB=∠FAC,故(4)正确,
只有AF平分∠BAC时,∠FAB=∠EAB正确,故(2)错误.
综上所述,正确的是(1)(3)(4)共3个.
故选C.
...
C
【解析】根据全等三角形对应边相等,全等三角形对应角相等结合图象解答即可.
∵△ABC≌△AEF,
∴AC=AF,EF=BC,∠EAF=∠BAC,故(1)(3)正确,
∴∠EAF-∠BAF=∠BAC-∠BAF,
即∠EAB=∠FAC,故(4)正确,
只有AF平分∠BAC时,∠FAB=∠EAB正确,故(2)错误.
综上所述,正确的是(1)(3)(4)共3个.
故选C.
... 
