0 319673 319681 319687 319691 319697 319699 319703 319709 319711 319717 319723 319727 319729 319733 319739 319741 319747 319751 319753 319757 319759 319763 319765 319767 319768 319769 319771 319772 319773 319775 319777 319781 319783 319787 319789 319793 319799 319801 319807 319811 319813 319817 319823 319829 319831 319837 319841 319843 319849 319853 319859 319867 366461
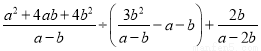 .
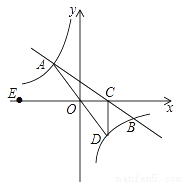
.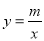 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n),OA=10,E为x轴负半轴上一点,且tan∠AOE=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n),OA=10,E为x轴负半轴上一点,且tan∠AOE=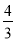 .
.
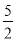 m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了
m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了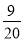 m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了
m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了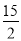 m%,求出m的值.
m%,求出m的值.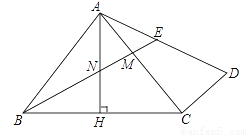
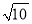 ,求△BMC的面积;
,求△BMC的面积;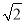 BN .
BN .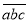 (a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的
(a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的 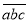 为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1. 与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,过点C作CD∥x轴,且交抛物线于点D,连接AD,交y轴于点E,连接AC.
与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,过点C作CD∥x轴,且交抛物线于点D,连接AD,交y轴于点E,连接AC.
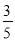 QE的值最小时,求此时PQ+
QE的值最小时,求此时PQ+ 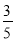 QE的值;
QE的值;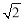 C.
C.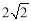 D.
D.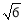
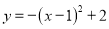 的图象与性质,下列说法正确的是( )
的图象与性质,下列说法正确的是( )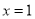 ,最小值是
,最小值是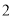 B. 对称轴是直线
B. 对称轴是直线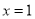 ,最大值是
,最大值是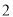
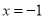 ,最小值是
,最小值是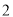 D. 对称轴是直线
D. 对称轴是直线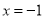 ,最大值是
,最大值是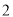
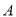 ,
, 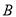 ,
, 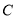 是⊙
是⊙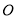 上的三个点,若
上的三个点,若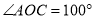 ,则
,则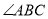 的度数为( ).
的度数为( ).
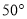 B.
B. 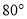 C.
C. 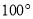 D.
D. 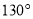

 B.
B.  C.
C.  D.
D. 