题目内容
如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.
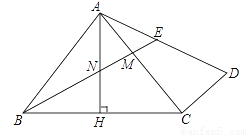
(1)若AB=3,AD=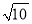 ,求△BMC的面积;
,求△BMC的面积;
(2)点E为AD的中点时,求证:AD=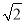 BN .
BN .
练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
题目内容
如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.

(1)若AB=3,AD=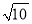 ,求△BMC的面积;
,求△BMC的面积;
(2)点E为AD的中点时,求证:AD=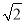 BN .
BN .
 小题狂做系列答案
小题狂做系列答案