0 319653 319661 319667 319671 319677 319679 319683 319689 319691 319697 319703 319707 319709 319713 319719 319721 319727 319731 319733 319737 319739 319743 319745 319747 319748 319749 319751 319752 319753 319755 319757 319761 319763 319767 319769 319773 319779 319781 319787 319791 319793 319797 319803 319809 319811 319817 319821 319823 319829 319833 319839 319847 366461
 转化为分数时,可设0.
转化为分数时,可设0. 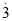 =
= 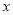 ,则
,则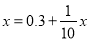 ,解得
,解得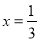 ,即0.
,即0. 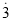 =
=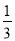 .仿此方法,将0.
.仿此方法,将0. 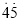 化成分数是_______.
化成分数是_______. ,
,  ,
,  ,
, 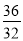 ,……中得到巴尔末公式,从而打开光谱奥妙的大门。请你根据以上光谱数据的规律写出它的第七个数据_______________.
,……中得到巴尔末公式,从而打开光谱奥妙的大门。请你根据以上光谱数据的规律写出它的第七个数据_______________. 的图象交于A(1,6),B(3,n)两点.
的图象交于A(1,6),B(3,n)两点.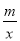 >0的解集;
>0的解集;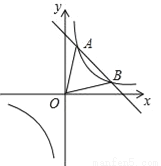
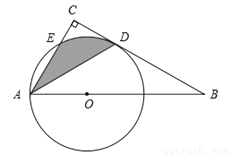
 上某一观测点M处,测得亭A在点M的北偏东30°方向, 亭B在点M的北偏东60°方向,当小明由点M沿小道
上某一观测点M处,测得亭A在点M的北偏东30°方向, 亭B在点M的北偏东60°方向,当小明由点M沿小道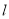 向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小明计算湖中两个小亭A、B之间的距离.
向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小明计算湖中两个小亭A、B之间的距离.
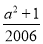 的值.
的值. 的值.
的值.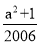 =
= .
.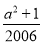 =-a-1+
=-a-1+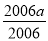 =-1,即a2-2007a+
=-1,即a2-2007a+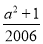 =-1.
=-1.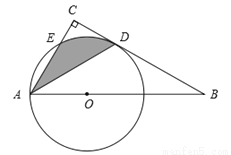
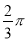 .
.
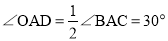 ,
,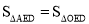
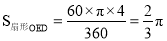 .
.