��Ŀ����
����֪��������ѭ��С��������ת��Ϊ���������磺��0. 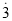 ת��Ϊ����ʱ������0.
ת��Ϊ����ʱ������0. 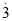 =
= 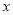 ����
����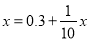 �����
�����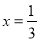 ����0.
����0. 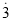 =
=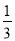 ���´˷�������0.
���´˷�������0. 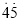 ���ɷ�����_______.
���ɷ�����_______.
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
����֪��������ѭ��С��������ת��Ϊ���������磺��0. 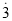 ת��Ϊ����ʱ������0.
ת��Ϊ����ʱ������0. 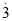 =
= 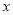 ����
����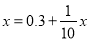 �����
�����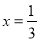 ����0.
����0. 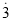 =
=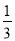 ���´˷�������0.
���´˷�������0. 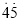 ���ɷ�����_______.
���ɷ�����_______.