��Ŀ����
��ͼ��Rt��ABC�У���BAC=60�㣬��OΪRt��ABCб��AB�ϵ�һ�㣬��OAΪ�뾶�ġ�O��BC���ڵ�D����AC���ڵ�E������AD.
��1�����CAD�Ķ�����
��2����OA = 2������Ӱ���ֵ��������������У�.
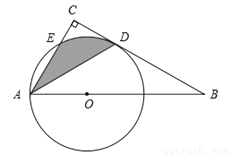
���𰸡���1����CAD�Ķ���Ϊ30�㣻
��2����Ӱ���ֵ����Ϊ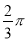 .
.
�������������������1������OD�������ߵ����ʿ�֪OD��BC���Ӷ���֤��AC��OD����ƽ���ߵ����ʺ͵��������ε����ʿ�֤����CAD=��OAD����2������OE��ED��OD����֤��ED��AO��Ȼ������ͬ�ȸߵ����������ε������ȿ�֪S��AED=S��EDO�����ǽ���Ӱ���ֵ������ת��Ϊ����EOD�������⼴�ɣ�
�����������1������OD��
��BC�ǡ�O�����ߣ�DΪ�е㣬
��OD��BC.
�֡�AC��BC��
��OD��AC��
���ADO=��CAD.
�֡�OD=OA��
���ADO=��OAD��
���CAD=��OAD=30��.
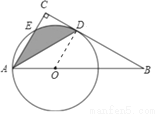
��2������OE��ED.
�ߡ�BAC=60�㣬OE=OA��
���OAEΪ�ȱ������Σ�
���AOE=60�㣬
���ADE=30��.
�֡�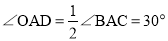 ��
��
���ADE=��OAD��
��ED��AO��
��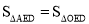
����Ӱ���ֵ���� = 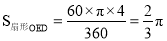 .
.
�����͡������
��������
6
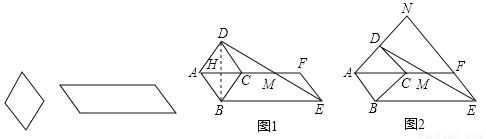
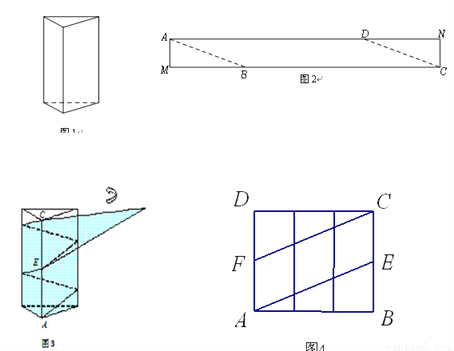
��ͼ����������������϶��ɵ�һ������ͼ�ε�����ͼ������ͼ������ߴ磨��λ��mm�������������ͼ�εı������
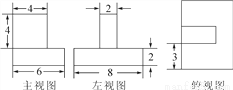
 �ŵ������ϵ�д�
�ŵ������ϵ�д�

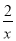 ����x��0ʱ������ͼ����( )
����x��0ʱ������ͼ����( )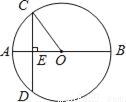

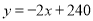 ��
��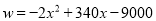 ����
����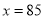 ʱ��
ʱ�� 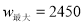 ��
��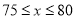 Ԫʱ����ȫ���ջ�Ͷ�ʵĻ�����ʹ�ڶ����µ�������1700Ԫ.
Ԫʱ����ȫ���ջ�Ͷ�ʵĻ�����ʹ�ڶ����µ�������1700Ԫ.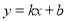 ������70��100������75��90��������ʽ�ã�
������70��100������75��90��������ʽ�ã�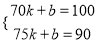 ��ã�
��ã� 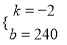 ����
����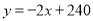 ��
��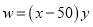
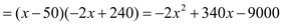 ����Ϊ����ʽ�ã�
����Ϊ����ʽ�ã� 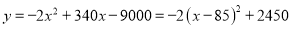 ����
����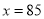 ʱ��
ʱ�� 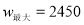
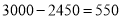 Ԫ��Ͷ�ʳɱ�û���ջأ���Ҫ����ȫ����Ͷ�ʵĻ�����ʹ�ڶ����µ�����ﵽ1700Ԫ�� ��
Ԫ��Ͷ�ʳɱ�û���ջأ���Ҫ����ȫ����Ͷ�ʵĻ�����ʹ�ڶ����µ�����ﵽ1700Ԫ�� ��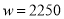 �ſ��ԣ��ɵ÷���
�ſ��ԣ��ɵ÷���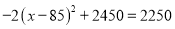 ����ã�
����ã� 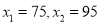 ��������
��������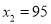 �������⣬Ӧ��ȥ.��
�������⣬Ӧ��ȥ.��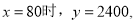 ����Ϊ-2<0���������߿������£���
����Ϊ-2<0���������߿������£���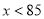 ʱ��
ʱ�� 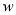 ��
��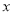 �����������
�����������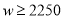 �������۵��۲�����80ʱ��
�������۵��۲�����80ʱ�� 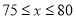
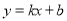 ������70��100������75��90��������ʽ�ã�
������70��100������75��90��������ʽ�ã�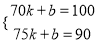 ��ã�
��ã� 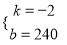 ����
����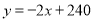 ��
��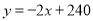
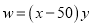
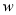 ��
��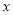 �Ĺ�ϵʽΪ
�Ĺ�ϵʽΪ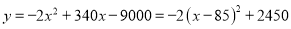
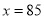 ʱ��
ʱ�� 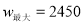
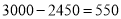 Ԫ��Ͷ�ʳɱ�û���ջأ�
Ԫ��Ͷ�ʳɱ�û���ջأ�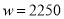 �ſ��ԣ�
�ſ��ԣ�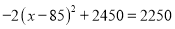 ����ã�
����ã� 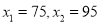
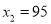 �������⣬Ӧ��ȥ.��
�������⣬Ӧ��ȥ.��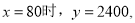 ��
��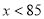 ʱ��
ʱ�� 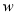 ��
��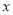 �����������
�����������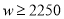 �������۵��۲�����80ʱ��
�������۵��۲�����80ʱ�� 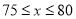
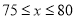 Ԫʱ����ȫ���ջ�Ͷ�ʵĻ�����ʹ�ڶ����µ�������1700Ԫ
Ԫʱ����ȫ���ջ�Ͷ�ʵĻ�����ʹ�ڶ����µ�������1700Ԫ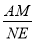 ��ֵ��
��ֵ��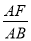 =k��kΪ����
=k��kΪ����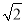 �ij�������ֱ���ú�k�Ĵ���ʽ��ʾ
�ij�������ֱ���ú�k�Ĵ���ʽ��ʾ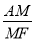 ��ֵ��
��ֵ��
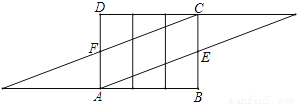
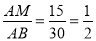 �����AMB=30�㣮
�����AMB=30�㣮 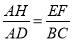 ��
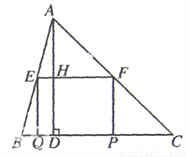
��
 ��ͼ����A��1��6����B��3��n�����㣮
��ͼ����A��1��6����B��3��n�����㣮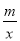 ��0�Ľ⼯��
��0�Ľ⼯��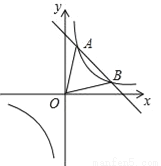

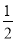 ��AOB
��AOB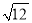 ��
��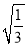 +
+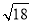 (2)
(2) 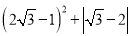
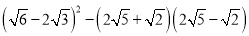 . ��4����-2��3+
. ��4����-2��3+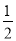 ��2004-
��2004-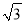 ��0-|-
��0-|-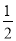 |
|