��Ŀ����
С����֪����������СͤA��B֮��ľ��룬������СͤA��Bλ��ͬһˮƽ���Ҷ�������ĺ���С��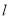 ��ijһ�۲��M�������ͤA�ڵ�M�ı�ƫ��30�㷽��, ͤB�ڵ�M�ı�ƫ��60�㷽��,��С���ɵ�M��С��
��ijһ�۲��M�������ͤA�ڵ�M�ı�ƫ��30�㷽��, ͤB�ڵ�M�ı�ƫ��60�㷽��,��С���ɵ�M��С��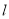 ����60��ʱ�������N������ʱ���ͤAǡ��λ�ڵ�N����������������30��ʱ�����Q������ʱͤBǡ��λ�ڵ�Q���������������ϲ������ݣ��������С�������������СͤA��B֮��ľ��룮
����60��ʱ�������N������ʱ���ͤAǡ��λ�ڵ�N����������������30��ʱ�����Q������ʱͤBǡ��λ�ڵ�Q���������������ϲ������ݣ��������С�������������СͤA��B֮��ľ��룮
��ϰ��ϵ�д�
�����Ŀ



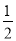 ABʱ����t��ֵ��
ABʱ����t��ֵ��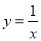 �����н����в���ȷ���ǣ� ��
�����н����в���ȷ���ǣ� ��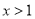 ʱ��
ʱ�� 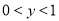 D. ��
D. ��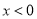 ʱ��y����x�����������
ʱ��y����x�����������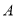 ��0��3����
��0��3����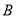 ����4��0����
����4��0����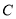 �ķ����������Ľ���ʽ��
�ķ����������Ľ���ʽ��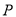 �ǣ�1����������ͼ����һ�㣬��
�ǣ�1����������ͼ����һ�㣬��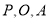 ����������ε�������COD�������ȣ����P�����꣮
����������ε�������COD�������ȣ����P�����꣮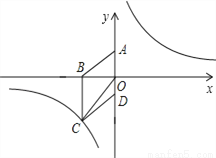
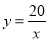 ����2��P��
����2��P��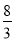 ��
�� 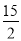 ����-
����-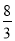 ��-
��-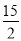 ����
���� 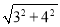 =5��
=5��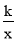 ��k��0����
��k��0����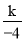 =-5�����k=20��
=-5�����k=20��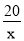 ��
��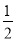 ��2��4=4��
��2��4=4��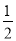 •OA•|x|=4��
•OA•|x|=4��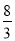 ��
��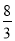 ����
����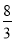 ʱ��y=
ʱ��y=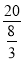 =
=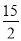 ����x=-
����x=-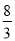 ʱ��y=
ʱ��y=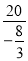 =-
=-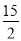 ��
��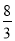 ��
�� 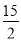 ����?
����?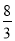 ��?
��?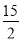 ����
����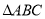 ��
�� 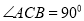 ����
����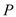 ��
��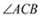 ���ߵľ�����ȣ���
���ߵľ�����ȣ��� ��
��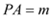 ��
��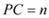 ������
������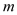 ��
��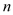 �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ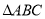 ���ܳ��������
���ܳ�������� ��
��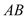 ���ڵ�
���ڵ�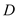 ����̽������
����̽������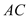 ��
��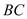 �ij��ȱ仯ʱ��
�ij��ȱ仯ʱ��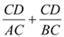 ��ֵ�Ƿ����仯�������䣬�������������ֵ�����仯����˵�����ɣ�
��ֵ�Ƿ����仯�������䣬�������������ֵ�����仯����˵�����ɣ�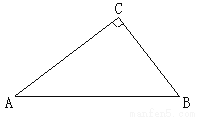

 �Ƿ���ҪŲ�ߣ���˵�����ɣ�
�Ƿ���ҪŲ�ߣ���˵�����ɣ�
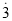 ת��Ϊ����ʱ������0.
ת��Ϊ����ʱ������0. 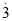 =
= 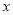 ����
����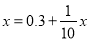 �����
�����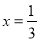 ����0.
����0. 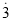 =
=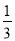 ���´˷�������0.
���´˷�������0. 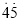 ���ɷ�����_______.
���ɷ�����_______.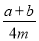 +m2��3cd=___________
+m2��3cd=___________