题目内容
设a是方程x2﹣2006x+1=0的一个根,求代数式a2﹣2007a+ 的值.
的值.
【答案】-1
【解析】【试题分析】根据方程的根的定义,则x=a代入方程,可得:a2-2006a+1=0,
所以a2-2006a=-1,a2+1=2006a,得a2﹣2007a+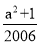 =
= .
.
【试题解析】
把x=a代入方程,可得:a2-2006a+1=0,
所以a2-2006a=-1,a2+1=2006a,
所以a2-2007a=-a-1,
所以a2-2007a+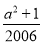 =-a-1+
=-a-1+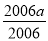 =-1,即a2-2007a+
=-1,即a2-2007a+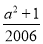 =-1.
=-1.
【方法点睛】本题目是一道考查一元二次方程的根的定义,方程的根满足该方程,代入得到相关代数式的值,进而将所求的额代数式进行转化,化简,求值.题目难度一般.
【题型】解答题
【结束】
5
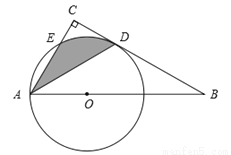
如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求∠CAD的度数;
(2)若OA = 2,求阴影部分的面积(结果保留π).
练习册系列答案
相关题目


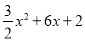 的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.
的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.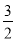 x2+6x+2<kx+b的解集;
x2+6x+2<kx+b的解集;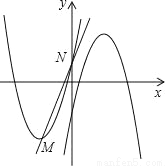
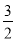 x2+6x﹣2(3)当q=
x2+6x﹣2(3)当q= 时,3﹣4q取最大值,最大值为﹣7
时,3﹣4q取最大值,最大值为﹣7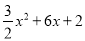 中x=0,则y=2,
中x=0,则y=2,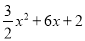 =
=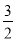 (x+2)2﹣4, ∴M(﹣2,﹣4).
(x+2)2﹣4, ∴M(﹣2,﹣4).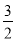 x2+6x+2<kx+b的解集为﹣2<x<0.
x2+6x+2<kx+b的解集为﹣2<x<0. 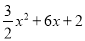 的顶点为M(﹣2,﹣4),
的顶点为M(﹣2,﹣4),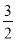 (x﹣2)2+4=﹣
(x﹣2)2+4=﹣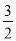 x2+6x﹣2.
x2+6x﹣2. 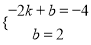 ,解得:
,解得: 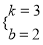 ,
,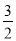 x2+6x﹣2=3x+2﹣q有实数根,即3x2﹣6x+8﹣2q有实数根,
x2+6x﹣2=3x+2﹣q有实数根,即3x2﹣6x+8﹣2q有实数根,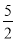 . ∵﹣4<0,
. ∵﹣4<0,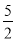 时,3﹣4q取最大值,最大值为﹣7.
时,3﹣4q取最大值,最大值为﹣7.
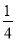 .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的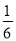 ,求道路的宽.
,求道路的宽.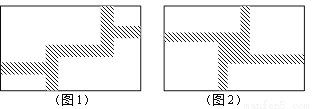
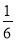 ,列方程求解即可.
,列方程求解即可.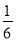 ×20×12,
×20×12,
 ,
,  ,
,  ,
, 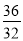 ,……中得到巴尔末公式,从而打开光谱奥妙的大门。请你根据以上光谱数据的规律写出它的第七个数据_______________.
,……中得到巴尔末公式,从而打开光谱奥妙的大门。请你根据以上光谱数据的规律写出它的第七个数据_______________.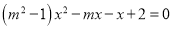 是关于x的一元一次方程,则代数式|m﹣1|的值为()
是关于x的一元一次方程,则代数式|m﹣1|的值为()