如图,在矩形ABCD中,AB=6m,BC=12m,点P从点A出发沿AB边向B以1m/s的速度运动,同时点Q从点B出发,沿BC边向点C以2m/s的速度运动,P、Q两点在分别到达B、C两点后就停止运动,设经过ts时,△PBQ的面积为Sm2,则
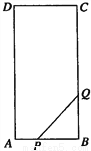
(1)S与t的函数解析式为:S=_________;
(2)用表格表示:
t/s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
S/m2 |
(3)用图象表示:
(4)在这个问题中,自变量t的取值范围是______;图象的对称轴是_______,顶点坐标是________;当t<______时,S的值随t值的增大而_______;当t>______时,S的值随t值的增大而_______(填“增大”或“减小”);当t=______时,S取得最大值为_______.
(1)-t2+6(2)填表见解析(3)图像见解析(4)0≤t≤6;t=3;(3,9);3;增大;3;减小;3;9 【解析】试题分析:(1)根据t秒时,P,Q两点的运动路程,分别表示PB,BQ的长度,可得△BPQ的面积S, (2)把t的值代入解析式可求得对应的S, (3)通过表格,描点,连线即可求解, (4)根据二次函数的图象性质可求解. 试题解析:(1)第t秒时,AP...
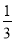 ,高为上底上的4倍还多1,如果下底为x,则梯形的面积S与下底x的函数关系式为________.
,高为上底上的4倍还多1,如果下底为x,则梯形的面积S与下底x的函数关系式为________.
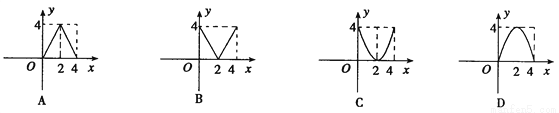

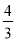 m2 B.
m2 B. 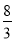 m2 C. 4m2 D.
m2 C. 4m2 D. 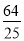 m2
m2