题目内容
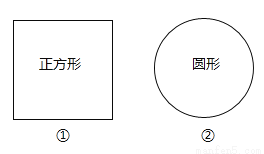
小亮同学想在房子附近开辟一块绿化场,现共有a米长的篱笆材料,他设计了两种方案:一种是围成正方形的场地,另一种是围成圆形的场地,那么选用哪一种方案围成的场地面积较大________(填序号).
练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
题目内容
小亮同学想在房子附近开辟一块绿化场,现共有a米长的篱笆材料,他设计了两种方案:一种是围成正方形的场地,另一种是围成圆形的场地,那么选用哪一种方案围成的场地面积较大________(填序号).

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案