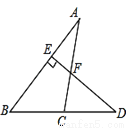
如图△ABC中，∠A：∠B=1：2，DE⊥AB于E，且∠FCD=75°，则∠D=________．
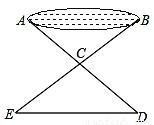
如图，要测量池塘两端A，B的距离，可先在平地上取一个可以直接到达A，B两点的C，连接AC并延长AC到点D，使CD=CA，连接BC并延长BC到点E，使CE=CB，连接DE，那么量出DE的长就等于AB的长，这是因为△ABC≌△DEC，而这个判定全等的依据是____________．
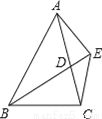
如图，已知，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA．下面结论：①△ABD≌△EBC；②AC=2CD；③AD=AE=EC；④∠BCE+∠BCD=180°．其中正确的是（ ）
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案已知：在△ABC中，∠A=60°，如要判定△ABC是等边三角形，还需添加一个条件．现有下面三种说法：
①如果添加条件“AB=AC”，那么△ABC是等边三角形；
②如果添加条件“∠B=∠C”，那么△ABC是等边三角形；
③如果添加条件“边AB、BC上的高相等”，那么△ABC是等边三角形．
上述说法中，正确的有（ ）
A. 3个 B. 2个 C. 1个 D. 0个
查看答案如图，在已知的△ABC中，按以下步骤作图：
①分别以B，C为圆心，以大于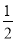
BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠A=50°，则∠ACB的度数为（ ）
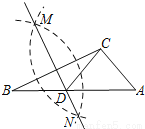
A. 90° B. 95° C. 100° D. 105°
查看答案如图，在△ABC中，AB=AC，D为BC上一点，且DA=DC，BD=BA，则∠B的大小为
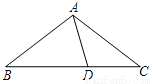
A. 40° B. 36° C. 30° D. 25°
查看答案 试题属性- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
等腰三角形的一个内角为80°，则顶角的度数是_________．
80°或20° 【解析】试题分析：分80°角是顶角与底角两种情况讨论求解． 试题解析：①80°角是顶角时，三角形的顶角为80°， ②80°角是底角时，顶角为180°-80°×2=20°， 综上所述，该等腰三角形顶角的度数为80°或20°．如图△ABC中，∠A：∠B=1：2，DE⊥AB于E，且∠FCD=75°，则∠D=________．
如图，要测量池塘两端A，B的距离，可先在平地上取一个可以直接到达A，B两点的C，连接AC并延长AC到点D，使CD=CA，连接BC并延长BC到点E，使CE=CB，连接DE，那么量出DE的长就等于AB的长，这是因为△ABC≌△DEC，而这个判定全等的依据是____________．
如图，已知，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA．下面结论：①△ABD≌△EBC；②AC=2CD；③AD=AE=EC；④∠BCE+∠BCD=180°．其中正确的是（ ）
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案已知：在△ABC中，∠A=60°，如要判定△ABC是等边三角形，还需添加一个条件．现有下面三种说法：
①如果添加条件“AB=AC”，那么△ABC是等边三角形；
②如果添加条件“∠B=∠C”，那么△ABC是等边三角形；
③如果添加条件“边AB、BC上的高相等”，那么△ABC是等边三角形．
上述说法中，正确的有（ ）
A. 3个 B. 2个 C. 1个 D. 0个
查看答案如图，在已知的△ABC中，按以下步骤作图：
①分别以B，C为圆心，以大于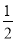BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠A=50°，则∠ACB的度数为（ ）
A. 90° B. 95° C. 100° D. 105°
查看答案 试题属性- 题型：填空题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
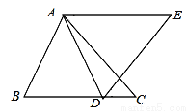
如图，在△ABC中，点D在BC上且AB=AD，AC=AE，∠BAD=∠CAE，DE=12，CD=4，则BD=_________．
等腰三角形的一个内角为80°，则顶角的度数是_________．
查看答案如图△ABC中，∠A：∠B=1：2，DE⊥AB于E，且∠FCD=75°，则∠D=________．
如图，要测量池塘两端A，B的距离，可先在平地上取一个可以直接到达A，B两点的C，连接AC并延长AC到点D，使CD=CA，连接BC并延长BC到点E，使CE=CB，连接DE，那么量出DE的长就等于AB的长，这是因为△ABC≌△DEC，而这个判定全等的依据是____________．
如图，已知，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA．下面结论：①△ABD≌△EBC；②AC=2CD；③AD=AE=EC；④∠BCE+∠BCD=180°．其中正确的是（ ）
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案已知：在△ABC中，∠A=60°，如要判定△ABC是等边三角形，还需添加一个条件．现有下面三种说法：
①如果添加条件“AB=AC”，那么△ABC是等边三角形；
②如果添加条件“∠B=∠C”，那么△ABC是等边三角形；
③如果添加条件“边AB、BC上的高相等”，那么△ABC是等边三角形．
上述说法中，正确的有（ ）
A. 3个 B. 2个 C. 1个 D. 0个
查看答案 试题属性- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
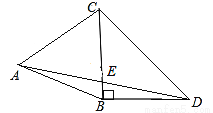
如图，△ABC是等边三角形，∠CBD=90°，BD=BC，连接AD交BC于点E，则∠AEC的度数是_________．
如图，在△ABC中，点D在BC上且AB=AD，AC=AE，∠BAD=∠CAE，DE=12，CD=4，则BD=_________．
等腰三角形的一个内角为80°，则顶角的度数是_________．
查看答案如图△ABC中，∠A：∠B=1：2，DE⊥AB于E，且∠FCD=75°，则∠D=________．
如图，要测量池塘两端A，B的距离，可先在平地上取一个可以直接到达A，B两点的C，连接AC并延长AC到点D，使CD=CA，连接BC并延长BC到点E，使CE=CB，连接DE，那么量出DE的长就等于AB的长，这是因为△ABC≌△DEC，而这个判定全等的依据是____________．
如图，已知，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA．下面结论：①△ABD≌△EBC；②AC=2CD；③AD=AE=EC；④∠BCE+∠BCD=180°．其中正确的是（ ）
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案 试题属性- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
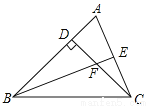
如图，在△ABC中，CD是AB边上高，BE为角平分线，若∠BFC=113°，求∠BCF的度数．
如图，△ABC是等边三角形，∠CBD=90°，BD=BC，连接AD交BC于点E，则∠AEC的度数是_________．
如图，在△ABC中，点D在BC上且AB=AD，AC=AE，∠BAD=∠CAE，DE=12，CD=4，则BD=_________．
等腰三角形的一个内角为80°，则顶角的度数是_________．
查看答案如图△ABC中，∠A：∠B=1：2，DE⊥AB于E，且∠FCD=75°，则∠D=________．
如图，要测量池塘两端A，B的距离，可先在平地上取一个可以直接到达A，B两点的C，连接AC并延长AC到点D，使CD=CA，连接BC并延长BC到点E，使CE=CB，连接DE，那么量出DE的长就等于AB的长，这是因为△ABC≌△DEC，而这个判定全等的依据是____________．
- 题型：解答题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
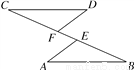
如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．
如图，在△ABC中，CD是AB边上高，BE为角平分线，若∠BFC=113°，求∠BCF的度数．
如图，△ABC是等边三角形，∠CBD=90°，BD=BC，连接AD交BC于点E，则∠AEC的度数是_________．
如图，在△ABC中，点D在BC上且AB=AD，AC=AE，∠BAD=∠CAE，DE=12，CD=4，则BD=_________．
等腰三角形的一个内角为80°，则顶角的度数是_________．
查看答案如图△ABC中，∠A：∠B=1：2，DE⊥AB于E，且∠FCD=75°，则∠D=________．
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图：△ABC和△ADE是等边三角形，AD是BC边上的中线．求证：BE=BD．
如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．
如图，在△ABC中，CD是AB边上高，BE为角平分线，若∠BFC=113°，求∠BCF的度数．
如图，△ABC是等边三角形，∠CBD=90°，BD=BC，连接AD交BC于点E，则∠AEC的度数是_________．
如图，在△ABC中，点D在BC上且AB=AD，AC=AE，∠BAD=∠CAE，DE=12，CD=4，则BD=_________．
等腰三角形的一个内角为80°，则顶角的度数是_________．
查看答案 试题属性- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
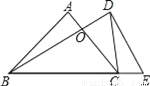
将一副直角三角板如图摆放，等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同，且斜边BC与BE在同一直线上，AC与BD交于点O，连接CD．
求证：△CDO是等腰三角形．
如图：△ABC和△ADE是等边三角形，AD是BC边上的中线．求证：BE=BD．
如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．
如图，在△ABC中，CD是AB边上高，BE为角平分线，若∠BFC=113°，求∠BCF的度数．
如图，△ABC是等边三角形，∠CBD=90°，BD=BC，连接AD交BC于点E，则∠AEC的度数是_________．
如图，在△ABC中，点D在BC上且AB=AD，AC=AE，∠BAD=∠CAE，DE=12，CD=4，则BD=_________．
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
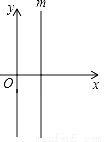
如图，在直角坐标平面内，已知点A（8，0），点B（3，0），点C是点A关于直线m（直线m上各点的横坐标都为3）的对称点．
（1）在图中标出点A，B，C的位置并求出点C的坐标；
（2）如果点P在y轴上，过点P作直线l∥x轴，点A关于直线l的对称点是点D，那么当△BCD的面积等于10时，求点P的坐标．
将一副直角三角板如图摆放，等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同，且斜边BC与BE在同一直线上，AC与BD交于点O，连接CD．
求证：△CDO是等腰三角形．
如图：△ABC和△ADE是等边三角形，AD是BC边上的中线．求证：BE=BD．
如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．
如图，在△ABC中，CD是AB边上高，BE为角平分线，若∠BFC=113°，求∠BCF的度数．
如图，△ABC是等边三角形，∠CBD=90°，BD=BC，连接AD交BC于点E，则∠AEC的度数是_________．
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
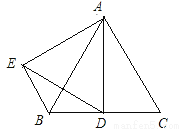
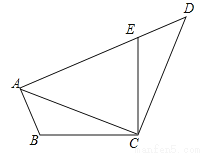
如图，已知在四边形ABCD中，点E在AD上，∠BCE=∠ACD=90°，∠BAC=∠D，BC=CE．
（1）求证：AC=CD；
（2）若AC=AE，求∠DEC的度数．
如图，在直角坐标平面内，已知点A（8，0），点B（3，0），点C是点A关于直线m（直线m上各点的横坐标都为3）的对称点．
（1）在图中标出点A，B，C的位置并求出点C的坐标；
（2）如果点P在y轴上，过点P作直线l∥x轴，点A关于直线l的对称点是点D，那么当△BCD的面积等于10时，求点P的坐标．
将一副直角三角板如图摆放，等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同，且斜边BC与BE在同一直线上，AC与BD交于点O，连接CD．
求证：△CDO是等腰三角形．
如图：△ABC和△ADE是等边三角形，AD是BC边上的中线．求证：BE=BD．
如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．
如图，在△ABC中，CD是AB边上高，BE为角平分线，若∠BFC=113°，求∠BCF的度数．
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧