题目内容
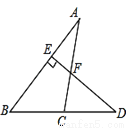
如图,在△ABC中,CD是AB边上高,BE为角平分线,若∠BFC=113°,求∠BCF的度数.
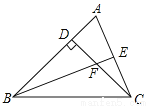
如图,△ABC是等边三角形,∠CBD=90°,BD=BC,连接AD交BC于点E,则∠AEC的度数是_________.
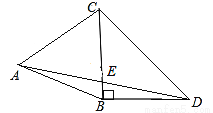
如图,在△ABC中,点D在BC上且AB=AD,AC=AE,∠BAD=∠CAE,DE=12,CD=4,则BD=_________.
等腰三角形的一个内角为80°,则顶角的度数是_________.
查看答案如图△ABC中,∠A:∠B=1:2,DE⊥AB于E,且∠FCD=75°,则∠D=________.
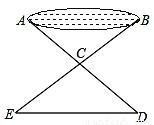
如图,要测量池塘两端A,B的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连接BC并延长BC到点E,使CE=CB,连接DE,那么量出DE的长就等于AB的长,这是因为△ABC≌△DEC,而这个判定全等的依据是____________.
- 题型:解答题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 名师点拨卷系列答案
名师点拨卷系列答案把下列各数填入相应的大括号内:
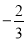 ,
, 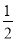 ,﹣0.01,
,﹣0.01, 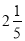 ,7,1,﹣(﹣4),+(﹣1)
,7,1,﹣(﹣4),+(﹣1)
正数集合{ …}
负数集合{ …}
非负整数集合{ …}
分数集合{ …}.
答案见解析. 【解析】试题分析:根据有理数的分类,结合正数、负数、非负整数、分数的特点分类即可. 试题解析:正数集合{, ,7,1,﹣(﹣4)…} 负数集合{,﹣0.01, +(﹣1)…} 非负整数集合{, ,7,1,﹣(﹣4)…} 分数集合{, ,﹣0.01, …}.把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长和是_____cm.(用m或n的式子表示).
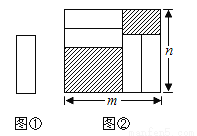
单项式﹣2xy5的系数是m,次数是n,则m﹣n=_____.
查看答案一列单项式﹣x2,3x3,﹣5x4,7x5.…,按此规律排列,则第9个单项式是_____.
查看答案在3,﹣4,6,﹣7这四个数中,任取两个数相乘,所得的积最大的是_____.
查看答案若a、b互为倒数,则(﹣ab)2017=_____.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
在平面直角坐标系中,若⊙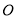 是以原点为圆心,
是以原点为圆心, 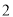 为半径的圆,则点
为半径的圆,则点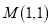 在( ).
在( ).
A. ⊙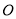 内 B. ⊙
内 B. ⊙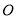 外 C. ⊙
外 C. ⊙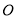 上 D. 不能确定
上 D. 不能确定
如图,已知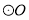 的半径
的半径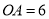 ,
, 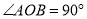 ,则
,则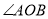 所对的弧
所对的弧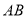 的长为( )
的长为( )
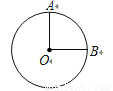
A. 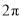 B.
B. 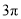 C.
C. 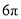 D.
D. 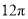
如图, 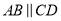 ,
, 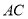 ,
, 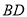 交于
交于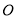 ,
, 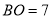 ,
, 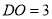 ,
, 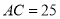 ,则
,则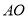 长为( ).
长为( ).
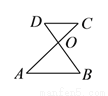
A. 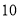 B.
B. 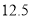 C.
C. 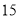 D.
D. 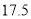
将抛物线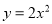 先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
A. 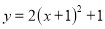 B.
B. 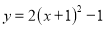 C.
C. 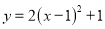 D.
D. 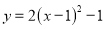
若二次函数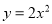 的图象经过点
的图象经过点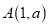 ,则
,则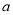 的值为( ).
的值为( ).
A. 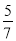 B.
B. 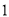 C.
C. 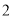 D.
D. 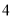
若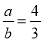 ,则
,则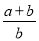 的值等于( ).
的值等于( ).
A. 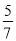 B.
B. 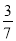 C.
C. 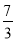 D.
D. 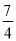
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
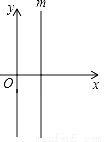
如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于直线m(直线m上各点的横坐标都为3)的对称点.
(1)在图中标出点A,B,C的位置并求出点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于10时,求点P的坐标.
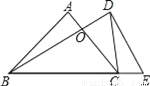
将一副直角三角板如图摆放,等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.
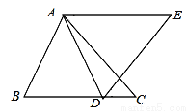
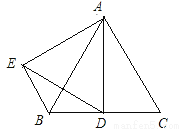
如图:△ABC和△ADE是等边三角形,AD是BC边上的中线.求证:BE=BD.
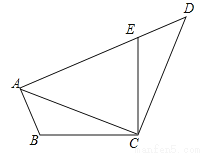
如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.
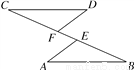
如图,在△ABC中,CD是AB边上高,BE为角平分线,若∠BFC=113°,求∠BCF的度数.

- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,要测量池塘两端A,B的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连接BC并延长BC到点E,使CE=CB,连接DE,那么量出DE的长就等于AB的长,这是因为△ABC≌△DEC,而这个判定全等的依据是____________.

如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下面结论:①△ABD≌△EBC;②AC=2CD;③AD=AE=EC;④∠BCE+∠BCD=180°.其中正确的是( )
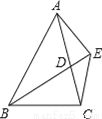
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案已知:在△ABC中,∠A=60°,如要判定△ABC是等边三角形,还需添加一个条件.现有下面三种说法:
①如果添加条件“AB=AC”,那么△ABC是等边三角形;
②如果添加条件“∠B=∠C”,那么△ABC是等边三角形;
③如果添加条件“边AB、BC上的高相等”,那么△ABC是等边三角形.
上述说法中,正确的有( )
A. 3个 B. 2个 C. 1个 D. 0个
查看答案如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于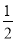 BC的长为半径作弧,两弧相交于两点M,N;
BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
若CD=AC,∠A=50°,则∠ACB的度数为( )
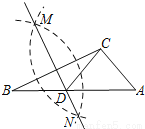
A. 90° B. 95° C. 100° D. 105°
查看答案如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为
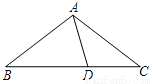
A. 40° B. 36° C. 30° D. 25°
查看答案如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确结论的个数是( )
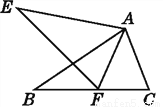
A. 1个 B. 2个 C. 3个 D. 4个
查看答案 试题属性- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于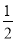 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
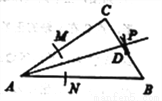
A. 15 B. 30 C. 45 D. 60
B 【解析】试题分析:由题意得AP是∠BAC的平分线,过点D作DE⊥AB于E,又∵∠C=90°,∴DE=CD,∴△ABD的面积=AB•DE=×15×4=30.故选B.下列条件中,不能判定两个直角三角形全等的是( )
A. 两直角边对应相等 B. 斜边和一条直角边对应相等
C. 两锐角对应相等 D. 一个锐角和斜边对应相等
查看答案一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数为( )
A. 7 B. 8 C. 9 D. 10
查看答案一副三角板如图叠放在一起,则图中∠α的度数为( )
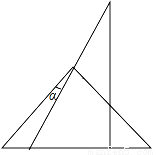
A. 35° B. 30° C. 25° D. 15°
查看答案如图,EA∥DF,AE=DF,要使△AEC≌△DFB,只要( )
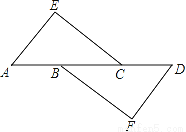
A. AB=CD B. EC=BF C. ∠A=∠D D. AB=BC
查看答案如图,已知在△ABC中,∠ABC=70°,∠C=50°,BD是角平分线,则∠BDC的度数为
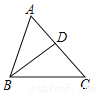
A. 95° B. 100° C. 110° D. 120°
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧


 x=6的是( )
x=6的是( )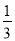 是6 B. x相反数的3倍是6
是6 B. x相反数的3倍是6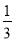 是6 D.
是6 D. 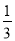 与一个数的差是6
与一个数的差是6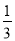 ,0,
,0, 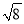 ,
, 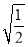 ,
,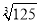 ,π,0.1010010001….
,π,0.1010010001….