若y与x3成反比例,且x=2时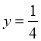 。
。
(1)求y与x的函数表达式;
(2)求y=—16时x的值。
(1)y= (2)x= 【解析】试题分析:(1)根据y与x3成反比例,可设,把x=2, ,代入可得k=2, 即可求出函数表达式,(2)把y=-16代入(1)中函数关系式即可求解. 试题解析:(1)因为y与x3成反比例, 则可设, 因为x=2, , 所以, 所以 (2)当 y=-16时,代入可得: ,解得: x=.如图,点A在双曲线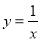 上,点B在双曲线
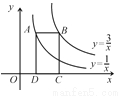
上,点B在双曲线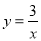 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.
上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.
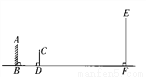
如图所示,冰冰在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为__________m。
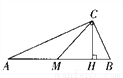
如图,在ΔABC中,∠ACB=90°,AC=7,BC=3,CM、CH 分别是中线和高,则SΔACM:SΔBCM = __________,SΔACH:SΔBCH = __________.
已知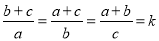 ,则抛物线
,则抛物线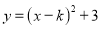 的顶点坐标为____________。
的顶点坐标为____________。
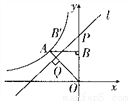
如图,反比例函数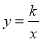 (k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )
(k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )
A. 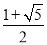 B.
B. 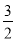 C.
C. 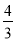 D.
D. 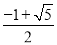
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图所示,一条河两岸有一段是平行的,在河的一岸每隔5米有一棵树,在河的对岸每隔50米有一根电线杆,在这岸离开岸边25米看对岸,看到对岸相邻两根电线杆恰被这岸的两棵树遮住,并且这两棵树之间还有三棵树,求河宽。
若y与x3成反比例,且x=2时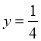 。
。
(1)求y与x的函数表达式;
(2)求y=—16时x的值。
查看答案如图,点A在双曲线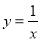 上,点B在双曲线
上,点B在双曲线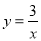 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.
上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.

如图所示,冰冰在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为__________m。

如图,在ΔABC中,∠ACB=90°,AC=7,BC=3,CM、CH 分别是中线和高,则SΔACM:SΔBCM = __________,SΔACH:SΔBCH = __________.

已知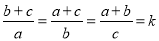 ,则抛物线
,则抛物线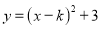 的顶点坐标为____________。
的顶点坐标为____________。
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,△ABC三个顶点坐标分别为A (1,2),B (3,1),C (2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.
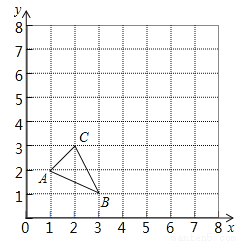
(1)在图中第一象限内画出符合要求的△A′B′C′;(不要求写画法)
(2)△A′B′C′的面积是: .
(1)作图见试题解析;(2)6. 【解析】 试题分析:(1)延长OA到A′,使OA′=2OA,同法得到其余点的对应点,顺次连接即可; (2)把所求三角形的面积分割为矩形的面积减去若干直角三角形的面积即可. 试题解析:(1) ; (2)△A′B′C′的面积=4×4﹣×2×2﹣×2×4﹣×2×4=6,故答案为:6.如图所示,一条河两岸有一段是平行的,在河的一岸每隔5米有一棵树,在河的对岸每隔50米有一根电线杆,在这岸离开岸边25米看对岸,看到对岸相邻两根电线杆恰被这岸的两棵树遮住,并且这两棵树之间还有三棵树,求河宽。

若y与x3成反比例,且x=2时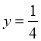 。
。
(1)求y与x的函数表达式;
(2)求y=—16时x的值。
查看答案如图,点A在双曲线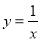 上,点B在双曲线
上,点B在双曲线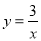 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.
上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.

如图所示,冰冰在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为__________m。

如图,在ΔABC中,∠ACB=90°,AC=7,BC=3,CM、CH 分别是中线和高,则SΔACM:SΔBCM = __________,SΔACH:SΔBCH = __________.

- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
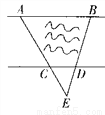
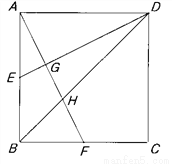
正方形ABCD中,E,F分别是AB与BC边上的中点,连接AF,DE,BD,交于G,H(如图所示)。求AG:GH:HF的值。
如图,△ABC三个顶点坐标分别为A (1,2),B (3,1),C (2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.

(1)在图中第一象限内画出符合要求的△A′B′C′;(不要求写画法)
(2)△A′B′C′的面积是: .
查看答案如图所示,一条河两岸有一段是平行的,在河的一岸每隔5米有一棵树,在河的对岸每隔50米有一根电线杆,在这岸离开岸边25米看对岸,看到对岸相邻两根电线杆恰被这岸的两棵树遮住,并且这两棵树之间还有三棵树,求河宽。

若y与x3成反比例,且x=2时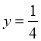 。
。
(1)求y与x的函数表达式;
(2)求y=—16时x的值。
查看答案如图,点A在双曲线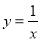 上,点B在双曲线
上,点B在双曲线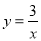 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.
上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.

如图所示,冰冰在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为__________m。

- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90º,E为AB的中点,求证:
(1)AC2=AB·AD;
(2)CE∥AD。
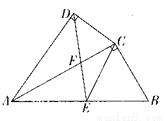
正方形ABCD中,E,F分别是AB与BC边上的中点,连接AF,DE,BD,交于G,H(如图所示)。求AG:GH:HF的值。

如图,△ABC三个顶点坐标分别为A (1,2),B (3,1),C (2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.

(1)在图中第一象限内画出符合要求的△A′B′C′;(不要求写画法)
(2)△A′B′C′的面积是: .
查看答案如图所示,一条河两岸有一段是平行的,在河的一岸每隔5米有一棵树,在河的对岸每隔50米有一根电线杆,在这岸离开岸边25米看对岸,看到对岸相邻两根电线杆恰被这岸的两棵树遮住,并且这两棵树之间还有三棵树,求河宽。

若y与x3成反比例,且x=2时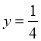 。
。
(1)求y与x的函数表达式;
(2)求y=—16时x的值。
查看答案如图,点A在双曲线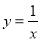 上,点B在双曲线
上,点B在双曲线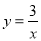 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.
上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.

- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
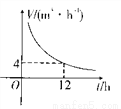
如图是某一蓄水池每1h的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数图象。
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出函数的函数表达式;
(3)若要6h排完水池的水,那么每1h的排水量应该是多少?
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90º,E为AB的中点,求证:
(1)AC2=AB·AD;
(2)CE∥AD。

正方形ABCD中,E,F分别是AB与BC边上的中点,连接AF,DE,BD,交于G,H(如图所示)。求AG:GH:HF的值。

如图,△ABC三个顶点坐标分别为A (1,2),B (3,1),C (2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.

(1)在图中第一象限内画出符合要求的△A′B′C′;(不要求写画法)
(2)△A′B′C′的面积是: .
查看答案如图所示,一条河两岸有一段是平行的,在河的一岸每隔5米有一棵树,在河的对岸每隔50米有一根电线杆,在这岸离开岸边25米看对岸,看到对岸相邻两根电线杆恰被这岸的两棵树遮住,并且这两棵树之间还有三棵树,求河宽。

若y与x3成反比例,且x=2时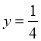 。
。
(1)求y与x的函数表达式;
(2)求y=—16时x的值。
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图, 正比例函数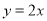 的图象与反比例函数
的图象与反比例函数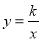 的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
(1)求k的值
(2)x轴上是否存在一点D,使ΔABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由。
如图是某一蓄水池每1h的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数图象。
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出函数的函数表达式;
(3)若要6h排完水池的水,那么每1h的排水量应该是多少?

如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90º,E为AB的中点,求证:
(1)AC2=AB·AD;
(2)CE∥AD。

正方形ABCD中,E,F分别是AB与BC边上的中点,连接AF,DE,BD,交于G,H(如图所示)。求AG:GH:HF的值。

如图,△ABC三个顶点坐标分别为A (1,2),B (3,1),C (2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.

(1)在图中第一象限内画出符合要求的△A′B′C′;(不要求写画法)
(2)△A′B′C′的面积是: .
查看答案如图所示,一条河两岸有一段是平行的,在河的一岸每隔5米有一棵树,在河的对岸每隔50米有一根电线杆,在这岸离开岸边25米看对岸,看到对岸相邻两根电线杆恰被这岸的两棵树遮住,并且这两棵树之间还有三棵树,求河宽。

- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想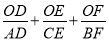 的值,并说明理由.
的值,并说明理由.
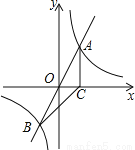
如图, 正比例函数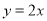 的图象与反比例函数
的图象与反比例函数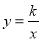 的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
(1)求k的值
(2)x轴上是否存在一点D,使ΔABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由。

如图是某一蓄水池每1h的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数图象。
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出函数的函数表达式;
(3)若要6h排完水池的水,那么每1h的排水量应该是多少?

如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90º,E为AB的中点,求证:
(1)AC2=AB·AD;
(2)CE∥AD。

正方形ABCD中,E,F分别是AB与BC边上的中点,连接AF,DE,BD,交于G,H(如图所示)。求AG:GH:HF的值。

如图,△ABC三个顶点坐标分别为A (1,2),B (3,1),C (2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.

(1)在图中第一象限内画出符合要求的△A′B′C′;(不要求写画法)
(2)△A′B′C′的面积是: .
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,已知∠MON=90º,A是∠MON内部的一点,过点A作AB⊥ON,垂点为点B,AB=3厘米,OB=4厘米,动点E、F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动。设运动时间为t秒(t>0)。
(1)当t=1秒时,ΔEOF与ΔABO是否相似?请说明理由。
(2)在运动过程中,不论t取何值时,总有EF⊥OA,为什么?
(3)连接AF,在运动过程中,是否存在某一时刻t,使得SΔAEF=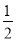 S四边形ABOF ?若存在,请求出此时t的值;若不存在,请说明理由。
S四边形ABOF ?若存在,请求出此时t的值;若不存在,请说明理由。
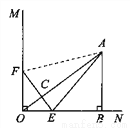
如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想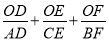 的值,并说明理由.
的值,并说明理由.

如图, 正比例函数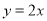 的图象与反比例函数
的图象与反比例函数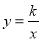 的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
(1)求k的值
(2)x轴上是否存在一点D,使ΔABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由。

如图是某一蓄水池每1h的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数图象。
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出函数的函数表达式;
(3)若要6h排完水池的水,那么每1h的排水量应该是多少?

如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90º,E为AB的中点,求证:
(1)AC2=AB·AD;
(2)CE∥AD。

正方形ABCD中,E,F分别是AB与BC边上的中点,连接AF,DE,BD,交于G,H(如图所示)。求AG:GH:HF的值。

- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列计算正确的是( ).
A. 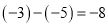 B.
B. 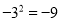 C.
C. 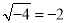 D.
D. 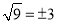
如图,已知∠MON=90º,A是∠MON内部的一点,过点A作AB⊥ON,垂点为点B,AB=3厘米,OB=4厘米,动点E、F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动。设运动时间为t秒(t>0)。
(1)当t=1秒时,ΔEOF与ΔABO是否相似?请说明理由。
(2)在运动过程中,不论t取何值时,总有EF⊥OA,为什么?
(3)连接AF,在运动过程中,是否存在某一时刻t,使得SΔAEF=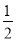 S四边形ABOF ?若存在,请求出此时t的值;若不存在,请说明理由。
S四边形ABOF ?若存在,请求出此时t的值;若不存在,请说明理由。

如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想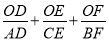 的值,并说明理由.
的值,并说明理由.

如图, 正比例函数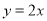 的图象与反比例函数
的图象与反比例函数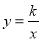 的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
(1)求k的值
(2)x轴上是否存在一点D,使ΔABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由。

如图是某一蓄水池每1h的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数图象。
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出函数的函数表达式;
(3)若要6h排完水池的水,那么每1h的排水量应该是多少?

如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90º,E为AB的中点,求证:
(1)AC2=AB·AD;
(2)CE∥AD。

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧