��Ŀ����
��y��x3�ɷ���������x=2ʱ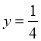 ��
��
��1����y��x�ĺ�������ʽ��
��2����y=��16ʱx��ֵ��
��1��y= ��2��x= ���������������:(1)����y��x3�ɷ�����,����,��x=2, ,����ɵ�k=2, ���������������ʽ,(2)��y=��16����(1)�к�����ϵʽ�������. �������:(1)��Ϊy��x3�ɷ�����, �����, ��Ϊx=2, , ����, ���� (2)�� y=��16ʱ,����ɵ�: ,���: x=.��ͼ����A��˫����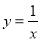 �ϣ���B��˫����
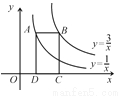
�ϣ���B��˫����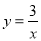 �ϣ���AB��x�ᣬC��D��x���ϣ����ı���ABCDΪ���Σ����������Ϊ__________��
�ϣ���AB��x�ᣬC��D��x���ϣ����ı���ABCDΪ���Σ����������Ϊ__________��
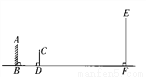
��ͼ��ʾ��������ǽ�Ϲ���һ�澵��AB�������ñ��CD������ͨ����˶����ھ����ϱ�ԵA��������˵Ķ���E��Ӱ�ӣ���֪AB=2m��CD=1.5m��BD=2m��BF=20m�������EF�ĸ߶�Ϊ__________m��
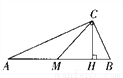
��ͼ���ڦ�ABC�У���ACB=90�㣬AC=7��BC=3��CM��CH �ֱ������ߺߣ���S��ACM��S��BCM = __________��S��ACH��S��BCH = __________.
��֪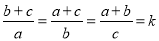 ����������
����������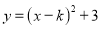 �Ķ�������Ϊ____________��
�Ķ�������Ϊ____________��
��ͼ������������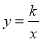 ��k��0����ͼ����A��-1��1��������A��AB��y�ᣬ����ΪB����y�����������ȡһ��P��0��t��������P��ֱ��OA�Ĵ���l����ֱ��lΪ�Գ��ᣬ��B����ԳƱ任�õ��˵�B���ڴ˷�����������ͼ���ϣ���t��ֵ�ǣ� ��
��k��0����ͼ����A��-1��1��������A��AB��y�ᣬ����ΪB����y�����������ȡһ��P��0��t��������P��ֱ��OA�Ĵ���l����ֱ��lΪ�Գ��ᣬ��B����ԳƱ任�õ��˵�B���ڴ˷�����������ͼ���ϣ���t��ֵ�ǣ� ��
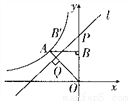
A. 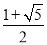 B.
B. 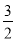 C.
C. 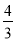 D.
D. 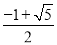
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д��������x�Ķ���ʽx2��kx+9��һ����ȫƽ��ʽ����ôk=________��
��6 ������������������߹���x�Ķ���ʽx2��kx+9��һ����ȫƽ��ʽ�� ��k=��6��a���෴���ǩ�3��b�ľ���ֵ��4����a+b=________��
�鿴����������ǻ������������ǵIJ���30�㣬��ô�ϴ�Ľ���________��
�鿴�����������뿪ԭ��4�����ȵ�λ�ĵ��ʾ������ ________ ��
�鿴����֪����ʽ2a3bn+1�멁3am��2b2��ͬ�����2m+3n=________��
�鿴��һ�е���ʽ����x2 �� 3x3 �� ��5x4 �� 7x5 �� �������˹������У����7������ʽΪ________
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
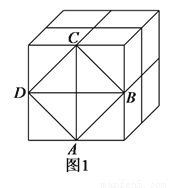
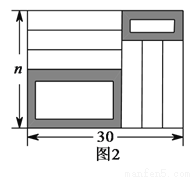
��ͼ1��������8��ͬ����С����������ɵ�ħ�������Ϊ64��
��1��������ħ�����ⳤ��
��2��ͼ����Ӱ������һ��������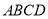 �������Ӱ���ֵ��������߳���
�������Ӱ���ֵ��������߳���
��3���������� �ŵ������ϣ���ͼ
�ŵ������ϣ���ͼ ��ʹ��
��ʹ�� ��
��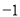 �غϣ���
�غϣ���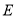 ��
��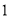 �غϣ���
�غϣ���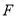 ���
���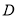 ����
����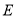 ��Գƣ���ô
��Գƣ���ô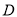 �������ϱ�ʾ����Ϊ__________����
�������ϱ�ʾ����Ϊ__________����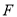 �������ϱ�ʾ����Ϊ__________��
�������ϱ�ʾ����Ϊ__________��
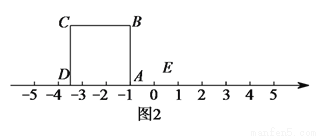
��������״��С��ȫ��ͬ��С�����ο�Ƭ�����н϶̵�һ�߳�Ϊ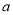 ���ף���ͼ
���ף���ͼ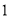 �����ص��ط���һ������Ϊ�����Σ���Ϊ
�����ص��ط���һ������Ϊ�����Σ���Ϊ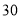 ���ף���Ϊ
���ף���Ϊ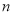 ���ף��ĺ��ӵײ�����ͼ
���ף��ĺ��ӵײ�����ͼ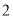 �������ӵ���δ����Ƭ���ǵIJ��ֱַ���
�������ӵ���δ����Ƭ���ǵIJ��ֱַ���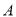 ��
��  ��ʾ����۲�ͼ�Σ��ش����⣺
��ʾ����۲�ͼ�Σ��ش����⣺
��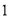 �������
������� �ij��Ϳ����ú�
�ij��Ϳ����ú� ��
��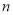 �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
�� ����ͼ�����鳤������Ӱ����
����ͼ�����鳤������Ӱ���� ��
�� 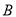 ���ܳ��ͣ��ú�
���ܳ��ͣ��ú�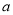 ��
�� �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
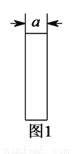
��֪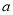 ��
��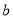 Ϊ����������������ʽ
Ϊ����������������ʽ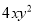 ��
�� 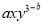 ��
��  ��ӵõ��ĺ���Ȼ�ǵ���ʽ����ô
��ӵõ��ĺ���Ȼ�ǵ���ʽ����ô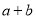 ��ֵ�����Ƕ��٣�����˵�����ɣ�
��ֵ�����Ƕ��٣�����˵�����ɣ�
�������ϱ�ʾ���и��������á�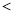 ��������������Ҫ����
��������������Ҫ����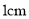 Ϊ��λ���Ȼ����ᣩ
Ϊ��λ���Ȼ����ᣩ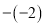 ��
��  ��
�� 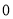 ��
�� 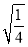 ��
�� 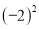 ��
��  ��
��
���㣺��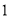 ��
��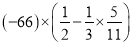 ��
��
��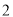 ��
��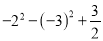 ��
��
��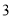 ��
�� ��
��
��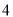 ��
��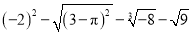 ��
��
��֪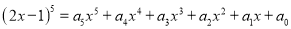 �ǹ���
�ǹ���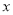 �ĺ��ʽ����
�ĺ��ʽ����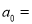 __________����
__________����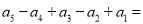 __________��
__________��
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
�����ϱ�ʾ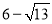 �ĵ�
�ĵ�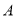 ��λ��Ӧ�ڣ� ����
��λ��Ӧ�ڣ� ����
A. 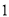 ��
��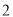 ֮�� B.
֮�� B. 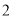 ��
��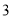 ֮�� C.
֮�� C. 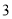 ��
��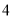 ֮�� D.
֮�� D. 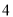 ��
��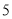 ֮��
֮��
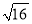 ��ƽ������ �� ��
��ƽ������ �� ��
A. 4 B. 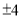 C.
C. 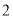 D.
D. 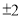
����������Ŀ�������̡�����Ĵ��š������Լ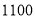 ������ң��ÿ�ѧ��������ʾ�� ����
������ң��ÿ�ѧ��������ʾ�� ����
A. 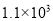 Ԫ B.
Ԫ B. 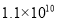 Ԫ C.
Ԫ C. 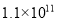 Ԫ D.
Ԫ D. 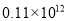 Ԫ
Ԫ
���м�����ȷ���ǣ� ����
A. 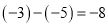 B.
B. 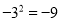 C.
C. 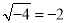 D.
D. 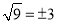
��ͼ����֪��MON=90º��A�ǡ�MON�ڲ���һ�㣬����A��AB��ON������Ϊ��B��AB=3���ף�OB=4���ף�����E��Fͬʱ��O���������E��1.5����/����ٶ���ON�����˶�����F��2����/����ٶ���OM�����˶���EF��OA���ڵ�C������AE������E�����Bʱ����F��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1����t=1��ʱ����EOF�릤ABO�Ƿ����ƣ���˵�����ɡ�
��2�����˶������У�����tȡ��ֵʱ������EF��OA��Ϊʲô��
��3������AF�����˶������У��Ƿ����ijһʱ��t��ʹ��S��AEF=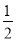 S�ı���ABOF �������ڣ��������ʱt��ֵ���������ڣ���˵�����ɡ�
S�ı���ABOF �������ڣ��������ʱt��ֵ���������ڣ���˵�����ɡ�
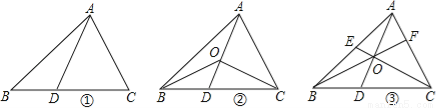
��ͼ���ڡ�ABC�У�D��BC���ϵĵ㣨�����B��C�غϣ�������AD��
�������룺
��1����ͼ�٣�����D��BC���ϵ��е�ʱ��S��ABD��S��ABC=�� ��������D��BC��������һ��ʱ��S��ABD��S��ABC=�� ������ͼ�������߶α�ʾ����
̽���о���
��2����ͼ�ڣ��ڡ�ABC�У�O�����߶�AD��һ�㣨�����A��D�غϣ�������BO��CO���Բ���S��BOC��S��ABC֮��Ӧ�õ���ͼ���������߶�֮�ȣ���˵�����ɣ�
��չӦ�ã�
��3����ͼ�ۣ�O���߶�AD��һ�㣨�����A��D�غϣ�������BO���ӳ���AC�ڵ�F������CO���ӳ���AB�ڵ�E���Բ���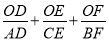 ��ֵ����˵�����ɣ�
��ֵ����˵�����ɣ�
- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
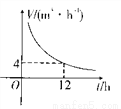
��ͼ��ijһ��ˮ��ÿ1h����ˮ��V��m3/h��������ˮ���е�ˮ����ʱ��t(h)֮��ĺ���ͼ��
��1���������ͼ���ṩ����Ϣ�������ˮ�ص���ˮ����
��2��д�������ĺ�������ʽ��
��3����Ҫ6h����ˮ�ص�ˮ����ôÿ1h����ˮ��Ӧ���Ƕ��٣�
��ͼ���ı���ABCD�У�ACƽ�֡�DAB����ADC=��ACB=90º��EΪAB���е㣬��֤��
��1��AC2=AB��AD��
��2��CE��AD��
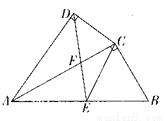
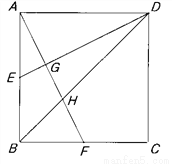
������ABCD�У�E��F�ֱ���AB��BC���ϵ��е㣬����AF��DE��BD������G��H����ͼ��ʾ������AG:GH:HF��ֵ��
��ͼ����ABC������������ֱ�ΪA ��1��2����B ��3��1����C ��2��3������ԭ��OΪλ�����ģ�����ABC�Ŵ�Ϊԭ����2���á�A��B��C�䣮
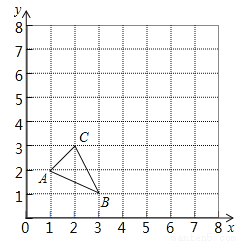
��1����ͼ�е�һ�����ڻ�������Ҫ��ġ�A��B��C�䣻����Ҫ��д������
��2����A��B��C�������ǣ� ��
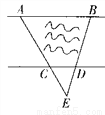
�鿴����ͼ��ʾ��һ����������һ����ƽ�еģ��ںӵ�һ��ÿ��5����һ�������ںӵĶ�ÿ��50����һ�����߸ˣ����ⰶ�뿪����25�����������������������߸�ǡ���ⰶ����������ס��������������֮�仹������������ӿ���
��y��x3�ɷ���������x=2ʱ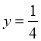 ��
��
��1����y��x�ĺ�������ʽ��
��2����y=��16ʱx��ֵ��
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ������������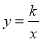 ��k��0����ͼ����A��-1��1��������A��AB��y�ᣬ����ΪB����y�����������ȡһ��P��0��t��������P��ֱ��OA�Ĵ���l����ֱ��lΪ�Գ��ᣬ��B����ԳƱ任�õ��˵�B���ڴ˷�����������ͼ���ϣ���t��ֵ�ǣ� ��
��k��0����ͼ����A��-1��1��������A��AB��y�ᣬ����ΪB����y�����������ȡһ��P��0��t��������P��ֱ��OA�Ĵ���l����ֱ��lΪ�Գ��ᣬ��B����ԳƱ任�õ��˵�B���ڴ˷�����������ͼ���ϣ���t��ֵ�ǣ� ��

A. 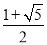 B.
B. 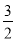 C.
C. 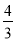 D.
D. 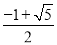
��ͼ��E��-4��2����F��-1��-1������OΪλ�����ģ���������1��2���ѡ�EOF��С�����E�Ķ�Ӧ��E�������Ϊ�� ����
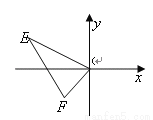
A. ��2��-1����-2��1�� B. ��8��-4����-8��4�� C. ��2��-1�� D. ��8��-4��
�鿴����ͼ��Rt��ABC�У���ACB=90�㣬��ABC=60�㣬BC=2cm��DΪBC���е㣬������E��1cm/s���ٶȴ�A�����������A��B��A�ķ����˶�����E����˶�ʱ��Ϊt�루0��t��6��������DE������BDE��ֱ��������ʱ��t��ֵΪ��������
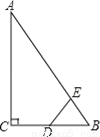
A. 2 B. 2.5��3.5 C. 3.5��4.5 D. 2��3.5��4.5
�鿴����ͼ���ڡ�ABC��, ��DE��BC , 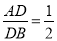 ,DE��4cm����BC�ij�Ϊ ( )
,DE��4cm����BC�ij�Ϊ ( )
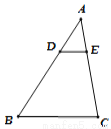
A. 8cm B. 12cm C. 11cm D. 10cm
�鿴����ͼ�����и�ʽ��ʹ��ACB�צ�DCA���ǣ� ��
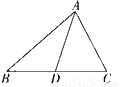
A. 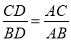 B.
B. 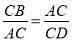 C.
C. 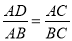 D.
D. 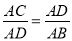
��ͬһƽ��ֱ������ϵ�У�һ�κ���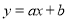
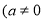 )�Ͷ��κ���
)�Ͷ��κ���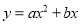
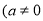 )��ͼ�����Ϊ�� ��
)��ͼ�����Ϊ�� ��
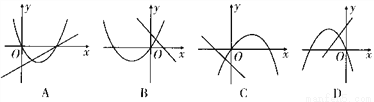
A. A B. B C. C D. D
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ�����
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
���ں���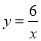 ������˵��������ǣ� ��
������˵��������ǣ� ��
A. ����ͼ���ڵ�һ��������
B. ����ͼ�������Գ�ͼ���������ĶԳ�ͼ��
C. ��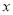 ��0ʱ��
��0ʱ�� 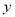 ��ֵ��
��ֵ��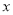 �����������
�����������
D. ��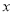 ��0ʱ��
��0ʱ�� 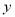 ��ֵ��
��ֵ��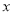 ���������С
���������С
���κ���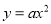 ��ͼ��һ�����㣨 ��
��ͼ��һ�����㣨 ��
A. ��0��0�� B. ��1��2�� C. ����1��2�� D. ���϶���ȷ
�鿴�����������߶��У�������ɱ����߶ε��ǣ� ��
A. 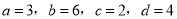
B. 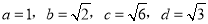
C. 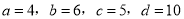
D. 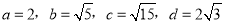
��ͼ����ƽ��ֱ������ϵ�У���֪������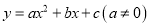 ��x���ཻ��
��x���ཻ��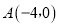 ��C����
��C���� ��y���ཻ�ڵ�B
��y���ཻ�ڵ�B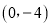 ��
��
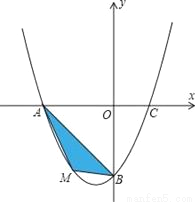
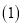 a 0��
a 0�� 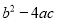
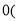 �
�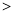 ����
����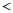 ��
�� 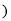 ��
��
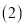 ���������߹���ֱ��
���������߹���ֱ��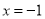 �Գƣ��������ߵĺ�������ʽ��
�Գƣ��������ߵĺ�������ʽ��
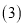 ��
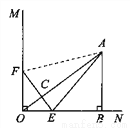
��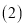 �������£�����MΪ������������������һ���㣬��M�ĺ�����Ϊ
�������£�����MΪ������������������һ���㣬��M�ĺ�����Ϊ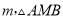 �����Ϊ
�����Ϊ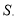 ��S����m�ĺ�����ϵʽ�������S�����ֵ��
��S����m�ĺ�����ϵʽ�������S�����ֵ��
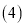 ��
��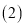 �������£�����P���������ϵĶ��㣬��Q��ֱ��
�������£�����P���������ϵĶ��㣬��Q��ֱ��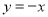 �ϵĶ��㣬�ж��м���λ���ܹ�ʹ�Ե�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
�ϵĶ��㣬�ж��м���λ���ܹ�ʹ�Ե�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
�Ķ����ϣ�����˼����С���ڽⷽ����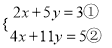 ʱ��������һ�֡�����������Ľⷨ��
ʱ��������һ�֡�����������Ľⷨ��
��������
������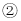 ����
���� 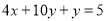 ��
��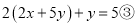
�ѷ��� ����
����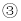 �ã�
�ã� 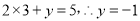
��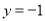 ����
���� ��
��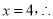 ������Ľ�Ϊ
������Ľ�Ϊ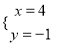 ��
��
�������������⣺
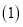 ģ��С���ġ�������������ⷽ����
ģ��С���ġ�������������ⷽ����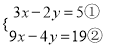
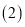 ��֪
��֪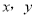 ���㷽����
���㷽����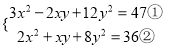 ��
��
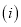 ��
��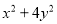 ��ֵ��
��ֵ��
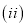 ��
��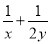 ��ֵ��
��ֵ��
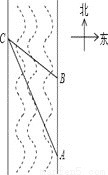
��2014��6��23�յ�ʮ�챣������ĸ��ͽ�����ϣ���ͼ��ʾ��ijͬѧΪ�˲��һ���ϱ�����ĺӶεĿ����ںӶ�����A���۲�Ӷ�ˮ����һ��C�����C��A��ƫ��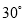 �ķ����ϣ��غӰ���ǰ��40����B�������C��B��ƫ��
�ķ����ϣ��غӰ���ǰ��40����B�������C��B��ƫ��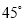 �ķ����ϣ���������������ݣ�����κӶεĿ���
�ķ����ϣ���������������ݣ�����κӶεĿ���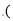 �����������
�����������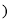
- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
���㣺 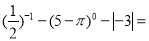 ��
��
��ͼ��ʾ����֪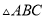 �У�
�У� 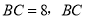 �ϵĸ�
�ϵĸ�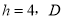 ΪBC��һ�㣬
ΪBC��һ�㣬 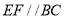 ����AB�ڵ�E����AC�ڵ�
����AB�ڵ�E����AC�ڵ�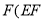 ����A��
����A��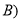 ����E��BC�ľ���Ϊx����
����E��BC�ľ���Ϊx����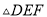 �����y����x�ĺ�����ͼ�����Ϊ
�����y����x�ĺ�����ͼ�����Ϊ ��
��
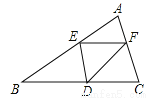
A. 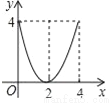 B.
B. 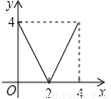
C. 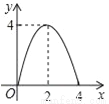 D.
D. 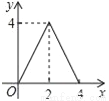
��50���ͺ�ΪL�ij����İ����л�����ͺ�ΪM�ij�����ÿ��20��������ÿ���л����M�ų����������
M�ų����� | 0 | 1 | 4 | 5 | 7 | 9 | 10 | 11 |
���� | 7 | 3 | 10 | 15 | 5 | 4 | 3 | 3 |
�����������ݣ�ѡ����ȷѡ� ��.
A. M�ų���һ����47��
B. �������ȡһ��������L�ų�����������9������¼�
C. �������ȡһ��������L�ų�����������4�ĸ���Ϊ0.26
D. ��50�����������һ�𣬴�������ó�һ��������ǡ����M�ŵĸ���Ϊ0.252
�鿴����ͼ������ABCD���ܳ�Ϊ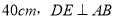 ������Ϊ
������Ϊ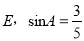 �������н�����ȷ����
�������н�����ȷ����
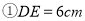 ��
�� 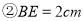 ��
�� 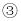 �������Ϊ
�������Ϊ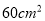 ��
�� 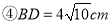 ��
��
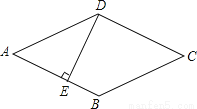
A. 1�� B. 2�� C. 3�� D. 4��
�鿴��Ϊִ�С�������������ߣ�ij��2014��Ͷ���������2500��Ԫ��Ԥ�Ƶ�2016��������ۼ�Ͷ��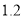 ��Ԫ
��Ԫ ��ÿ��Ͷ��������ѵ���ƽ�������ٷ���Ϊx�������з�����ȷ����
��ÿ��Ͷ��������ѵ���ƽ�������ٷ���Ϊx�������з�����ȷ����
A. 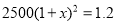
B. 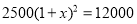
C. 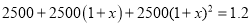
D. 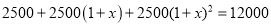
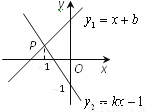
��ͼ��ʾ��ֱ��y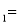 x
x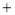 b��y
b��y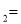 kx
kx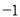 �ཻ�ڵ�P����P�ĺ�����Ϊ
�ཻ�ڵ�P����P�ĺ�����Ϊ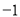 �������x�IJ� ��ʽx
�������x�IJ� ��ʽx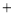 b
b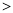 kx
kx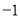 �Ľ⼯�������ϱ�ʾ��ȷ����
�Ľ⼯�������ϱ�ʾ��ȷ����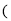
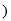
A. 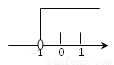
B. 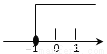
C. 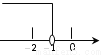
D. 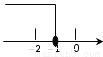
- ���ͣ������
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
�ⷽ�̣� 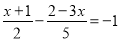
���㣺 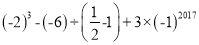
��������a��b��c�������ϵ�λ����ͼ��ʾ�����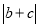 -
-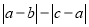 �Ľ��Ϊ__________.
�Ľ��Ϊ__________.

�Ѷ���ʽa-3b+c-2d�ĺ�3����������������������ǰ�����-���ţ����ý����_______.
�鿴����д��һ����Ϊx=-3��һԪһ�η��̣������____________________.
�鿴��-5�ľ���ֵΪ__________.
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������

