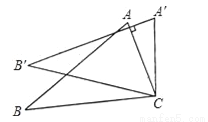
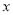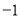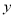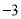如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( )
A. 50° B. 60° C. 70° D. 80°
C 【解析】试题分析:∵△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,∴∠BCB′=∠ACA′=20°,∵AC⊥A′B′,∴∠BAC=∠A′=90°﹣20°=70°.故选C.关于x的一元二次方程x2﹣6x+2k=0有两个不相等的实数根,则实数k的取值范围是( )
A. k≤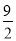 B. k<
B. k<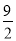 C. k≥
C. k≥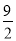 D. k>
D. k>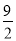
抛物线y=﹣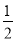 x2﹣x的顶点坐标是( )
x2﹣x的顶点坐标是( )
A. (1,﹣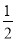 ) B. (﹣1,
) B. (﹣1, 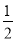 ) C. (
) C. (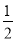 ,﹣1) D. (1,0)
,﹣1) D. (1,0)
4张扑克牌如图(1)所示放在桌子上,小敏把其中两张旋转180°后得到如图(2)所示,那么她所旋转的牌从左起是( )

A.第一张、第二张
B.第二张、第三张
C.第三张、第四张
D.第四张、第一张
查看答案已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
| … |
| 0 | 1 | 3 | … |
| … |
| 1 | 3 | 1 | … |
则下列判断中正确的是( )
A. 抛物线开口向上 B. 抛物线与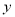 轴交于负半轴
轴交于负半轴
C. 当x=4时,y>0 D. 方程ax2+bx+c=0的正根在3与4之间
查看答案对于抛物线y=-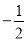 (x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,其中正确结论的个数是( )
(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣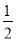 ,y2)、点C(
,y2)、点C(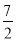 ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
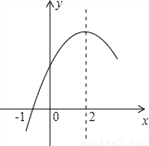
A. 2个 B. 3个 C. 4个 D. 5个
B 【解析】试题分析:由﹣=2,可得4a+b=0.故(1)正确;当x=﹣3时,y<0,所以9a﹣3b+c<0,即9a+c<3b,故(2)错误;由图象可知抛物线经过(﹣1,0)和(5,0),可得,解得,所以8a+7b+2c=8a﹣28a﹣10a=﹣30a,又因a<0,所以8a+7b=2c>0,故(3)正确.已知点A(﹣3,y1)、点B(﹣,y2)、点C(,y3),计算﹣2=,2﹣(﹣)=,因<...如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( )

A. 50° B. 60° C. 70° D. 80°
查看答案关于x的一元二次方程x2﹣6x+2k=0有两个不相等的实数根,则实数k的取值范围是( )
A. k≤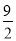 B. k<
B. k<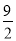 C. k≥
C. k≥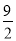 D. k>
D. k>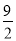
抛物线y=﹣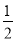 x2﹣x的顶点坐标是( )
x2﹣x的顶点坐标是( )
A. (1,﹣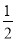 ) B. (﹣1,
) B. (﹣1, 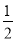 ) C. (
) C. (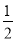 ,﹣1) D. (1,0)
,﹣1) D. (1,0)
4张扑克牌如图(1)所示放在桌子上,小敏把其中两张旋转180°后得到如图(2)所示,那么她所旋转的牌从左起是( )

A.第一张、第二张
B.第二张、第三张
C.第三张、第四张
D.第四张、第一张
查看答案已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
| … |
| 0 | 1 | 3 | … |
| … |
| 1 | 3 | 1 | … |
则下列判断中正确的是( )
A. 抛物线开口向上 B. 抛物线与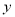 轴交于负半轴
轴交于负半轴
C. 当x=4时,y>0 D. 方程ax2+bx+c=0的正根在3与4之间
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
三角形两边长分别为3和6,第三边是方程x2﹣13x+36=0的根,则三角形的周长为 .
13 【解析】 试题分析:利用因式分解法解方程得到x1=4,x2=9,再利用三角形三边的关系得到x=4,然后计算三角形的周长. 【解析】 (x﹣4)(x﹣9)=0, x﹣4=0或x﹣9=0, 所以x1=4,x2=9, 因为3+6=9, 所以第三边长为4, 所以三角形的周长为3+6+4=13. 故答案为13.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣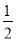 ,y2)、点C(
,y2)、点C(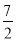 ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( )

A. 50° B. 60° C. 70° D. 80°
查看答案关于x的一元二次方程x2﹣6x+2k=0有两个不相等的实数根,则实数k的取值范围是( )
A. k≤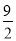 B. k<
B. k<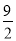 C. k≥
C. k≥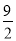 D. k>
D. k>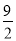
抛物线y=﹣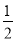 x2﹣x的顶点坐标是( )
x2﹣x的顶点坐标是( )
A. (1,﹣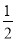 ) B. (﹣1,
) B. (﹣1, 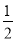 ) C. (
) C. (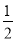 ,﹣1) D. (1,0)
,﹣1) D. (1,0)
4张扑克牌如图(1)所示放在桌子上,小敏把其中两张旋转180°后得到如图(2)所示,那么她所旋转的牌从左起是( )

A.第一张、第二张
B.第二张、第三张
C.第三张、第四张
D.第四张、第一张
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
右图是“靠右侧通道行驶”的交通标志,若将图案绕其中心顺时针旋转90°,则得到的图案是“ ”的交通标志(不画图案,只填含义).

三角形两边长分别为3和6,第三边是方程x2﹣13x+36=0的根,则三角形的周长为 .
查看答案二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣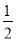 ,y2)、点C(
,y2)、点C(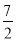 ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( )

A. 50° B. 60° C. 70° D. 80°
查看答案关于x的一元二次方程x2﹣6x+2k=0有两个不相等的实数根,则实数k的取值范围是( )
A. k≤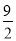 B. k<
B. k<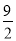 C. k≥
C. k≥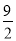 D. k>
D. k>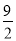
抛物线y=﹣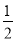 x2﹣x的顶点坐标是( )
x2﹣x的顶点坐标是( )
A. (1,﹣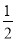 ) B. (﹣1,
) B. (﹣1, 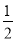 ) C. (
) C. (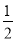 ,﹣1) D. (1,0)
,﹣1) D. (1,0)
- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若函数y=(a﹣1)x2﹣4x+2a的图象与x轴有且只有一个交点,则a的值为_____.
﹣1或2或1 【解析】∵函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个交点, 当函数为二次函数时,b2-4ac=16-4(a-1)×2a=0, 解得:a1=-1,a2=2, 当函数为一次函数时,a-1=0,解得:a=1. 故答案为:-1或2或1.右图是“靠右侧通道行驶”的交通标志,若将图案绕其中心顺时针旋转90°,则得到的图案是“ ”的交通标志(不画图案,只填含义).

三角形两边长分别为3和6,第三边是方程x2﹣13x+36=0的根,则三角形的周长为 .
查看答案二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣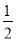 ,y2)、点C(
,y2)、点C(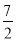 ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( )

A. 50° B. 60° C. 70° D. 80°
查看答案关于x的一元二次方程x2﹣6x+2k=0有两个不相等的实数根,则实数k的取值范围是( )
A. k≤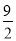 B. k<
B. k<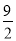 C. k≥
C. k≥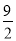 D. k>
D. k>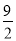
- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为_____.
y=x2﹣2x﹣3 【解析】先求出y=x2-2x+1和y=2x-2的交点C′的坐标为(1,4),再求出“梦之星”抛物线y=x2+2x+1的顶点A坐标(-1,0),接着利用点C和点C′关于x轴对称得到C(1,-4),则可设顶点式y=a(x-1)2-4然后把A点代入求出a的值即可得到原抛物线解析式. 【解析】 ∵y=x2-2x+1=(x+1)2,∴点A的坐标为(-1,0), 解方程...若函数y=(a﹣1)x2﹣4x+2a的图象与x轴有且只有一个交点,则a的值为_____.
查看答案右图是“靠右侧通道行驶”的交通标志,若将图案绕其中心顺时针旋转90°,则得到的图案是“ ”的交通标志(不画图案,只填含义).

三角形两边长分别为3和6,第三边是方程x2﹣13x+36=0的根,则三角形的周长为 .
查看答案二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣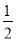 ,y2)、点C(
,y2)、点C(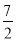 ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( )

A. 50° B. 60° C. 70° D. 80°
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
解一元二次方程
(1)x2﹣2x﹣1=0
(2)(2x﹣3)2=(x+2)2.
(1)x1=1﹣,x2=1+;(2)x1=,x2=5. 【解析】试题分析:(1)根据公式法可求方程的解; (2)先移项,然后通过平方差公式对等式的左边进行因式分解,化为两个一元一次方程求解即可. 试题解析:(1)x2﹣2x﹣1=0, △=(﹣2)2﹣4×1×(﹣1)=8, ∴, 即x1=1﹣,x2=1+ (2)(2x﹣3)2=(x+2)2, (2x﹣...已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为_____.
查看答案若函数y=(a﹣1)x2﹣4x+2a的图象与x轴有且只有一个交点,则a的值为_____.
查看答案右图是“靠右侧通道行驶”的交通标志,若将图案绕其中心顺时针旋转90°,则得到的图案是“ ”的交通标志(不画图案,只填含义).

三角形两边长分别为3和6,第三边是方程x2﹣13x+36=0的根,则三角形的周长为 .
查看答案二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣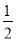 ,y2)、点C(
,y2)、点C(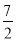 ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案 试题属性- 题型:解答题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
实践与操作:一般地,如果把一个图形绕着一个定点旋转一定角度α(α小于360°)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心,α叫做这个旋转对称图形的一个旋转角,请根据上述规定解答下列问题:
(1)请写出一个有一个旋转角是90°旋转对称图形,这个图形可以是_____;
(2)尺规作图:在图中的等边三角形内部作出一个图形,使作出的图形和这个等边三角形构成的整体既是一个旋转对称图形又是一个轴对称图形(作出的图形用实线,作图过程用虚线,保留痕迹,不写做法).
解一元二次方程
(1)x2﹣2x﹣1=0
(2)(2x﹣3)2=(x+2)2.
查看答案已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为_____.
查看答案若函数y=(a﹣1)x2﹣4x+2a的图象与x轴有且只有一个交点,则a的值为_____.
查看答案右图是“靠右侧通道行驶”的交通标志,若将图案绕其中心顺时针旋转90°,则得到的图案是“ ”的交通标志(不画图案,只填含义).

三角形两边长分别为3和6,第三边是方程x2﹣13x+36=0的根,则三角形的周长为 .
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).
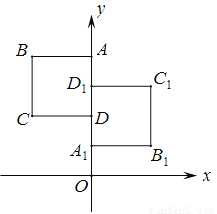
(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
(0, );B(-2,4)C(-2,2)(2,1)(2,3). 【解析】试题分析:(1)根据对称中心的性质,可得对称中心的坐标是D1D的中点,据此解答即可. (2)首先根据A,D的坐标分别是(0,4),(0,2),求出正方形ABCD与正方形A1B1C1D1的边长是多少,然后根据A,D1,D三点的坐标分别是(0,4),(0,3),(0,2),判断出顶点B,C,B1,C1的坐标各是多少即可...实践与操作:一般地,如果把一个图形绕着一个定点旋转一定角度α(α小于360°)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心,α叫做这个旋转对称图形的一个旋转角,请根据上述规定解答下列问题:
(1)请写出一个有一个旋转角是90°旋转对称图形,这个图形可以是_____;
(2)尺规作图:在图中的等边三角形内部作出一个图形,使作出的图形和这个等边三角形构成的整体既是一个旋转对称图形又是一个轴对称图形(作出的图形用实线,作图过程用虚线,保留痕迹,不写做法).

解一元二次方程
(1)x2﹣2x﹣1=0
(2)(2x﹣3)2=(x+2)2.
查看答案已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为_____.
查看答案若函数y=(a﹣1)x2﹣4x+2a的图象与x轴有且只有一个交点,则a的值为_____.
查看答案右图是“靠右侧通道行驶”的交通标志,若将图案绕其中心顺时针旋转90°,则得到的图案是“ ”的交通标志(不画图案,只填含义).

- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?
4株或者5株. 【解析】 试题分析:由已知假设每盆花苗增加x株,则每盆花苗有(x+3)株,得出平均单株盈利为(3﹣0.5x)元,由题意得(x+3)(3﹣0.5x)=10求出即可. 试题解析:【解析】 设每盆花苗增加x株,则每盆花苗有(x+3)株,平均单株盈利为:(3﹣0.5x)元,由题意得:(x+3)(3﹣0.5x)=10. 化简,整理,的. 解这个方程,得,,则3...如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).

(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
查看答案实践与操作:一般地,如果把一个图形绕着一个定点旋转一定角度α(α小于360°)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心,α叫做这个旋转对称图形的一个旋转角,请根据上述规定解答下列问题:
(1)请写出一个有一个旋转角是90°旋转对称图形,这个图形可以是_____;
(2)尺规作图:在图中的等边三角形内部作出一个图形,使作出的图形和这个等边三角形构成的整体既是一个旋转对称图形又是一个轴对称图形(作出的图形用实线,作图过程用虚线,保留痕迹,不写做法).

解一元二次方程
(1)x2﹣2x﹣1=0
(2)(2x﹣3)2=(x+2)2.
查看答案已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为_____.
查看答案若函数y=(a﹣1)x2﹣4x+2a的图象与x轴有且只有一个交点,则a的值为_____.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧