6．一元二次方程4x2-x=1的解是（ ）
| A． | x=0 | B． | x1=0，x2=4 | ||
| C． | x1=0，x2=$\frac{1}{4}$ | D． | x1=$\frac{1+\sqrt{17}}{8}$，x2=$\frac{1-\sqrt{17}}{8}$ |
5．数学翻译 牛顿是举世闻名的伟大数学家、物理学家，他创立了微积分（另一个创立者是莱布尼茨）、经典力学，在代数学、光学、天文学等方面也作出了重要贡献，牛顿用数学的语言、方法描述和研究自然规律，他呕心沥血，写成的光辉著作《自然哲学的数学原理》，照亮了人类科学文明的大道，牛顿在他的《普遍的算术》一书中写道：“要解答一个含有数量间的抽象关系的问题，只要把题目由日常的语言译成代数的语言就行了．”下表是由牛顿给出的1个例子改写、简化而成的，请将表的空白补上（不必化简）．
根据上表中的（3）可解得x=400．
| 日常语言 | 代数语言 |
| 一个商人有一笔钱 | x |
| 第一年他花去了100镑 | x-100 |
| 补进去余额的$\frac{1}{3}$ | （x-100）+$\frac{1}{3}$（x-100） |
| 第二年他又花去了100镑 | （1）（x-100）+$\frac{1}{3}$（x-100）-100 |
| 又补进去余额的$\frac{1}{3}$ | （2）（x-100）+$\frac{1}{3}$（x-100）-100+$\frac{1}{3}$[（x-100）+$\frac{1}{3}$（x-100）-100] |
| 结果他的钱数正好是原来的钱数 | （3）（x-100）+$\frac{1}{3}$（x-100）-100+$\frac{1}{3}$[（x-100）+$\frac{1}{3}$（x-100）-100]=x |
4．某通讯公司推出移动电话的两种计费方式（详请见下表）
温馨提示：若选用方式一，每月固定交费58元，当主动打出电话月累计时间不超过150分，不再额外交费；当超过150分，超过部分加收0.25元．
设一个月内使用移动电话主叫的时间为t分（t为正整数），
请根据表中提供的信息回答下列问题：
（1）用含有t的式子填写下表：
（2）当t=270时，哪种计费方式更省钱？请通过计算说明你的理由．
（3）当t＞350时，请选择哪一种说法最合理B
A．方式一计费省钱 B．方式二计费省钱
C．两种方式计费相同 D．无法判定．
0 311542 311550 311556 311560 311566 311568 311572 311578 311580 311586 311592 311596 311598 311602 311608 311610 311616 311620 311622 311626 311628 311632 311634 311636 311637 311638 311640 311641 311642 311644 311646 311650 311652 311656 311658 311662 311668 311670 311676 311680 311682 311686 311692 311698 311700 311706 311710 311712 311718 311722 311728 311736 366461
| 固定交费 | 主叫限定 时间/分 | 主叫超时费 （元/分） | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免费 |
| 方式二 | 88 | 350 | 0.19 | 免费 |
设一个月内使用移动电话主叫的时间为t分（t为正整数），
请根据表中提供的信息回答下列问题：
（1）用含有t的式子填写下表：
| t≤150 | 150＜t＜350 | t=350 | t＞350 | |
| 方式一计费/元 | 58 | 0.25t+20.5 | 108 | 0.25t+20.5 |
| 方式二计费/元 | 88 | 88 | 88 | 0.19t+21.5 |
（3）当t＞350时，请选择哪一种说法最合理B
A．方式一计费省钱 B．方式二计费省钱
C．两种方式计费相同 D．无法判定．
已知数a，b，c在数轴上的位置如图所示，化简|a+2b|-|c-2b|的结果是a+c．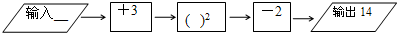
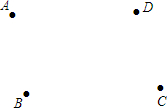如图，A，B，C，D是四个鱼塘的位置，要用一个供水泵向这四个鱼塘供水，为了使供水管最短，供水泵应建在什么位置？画出图形并说明理由．