15.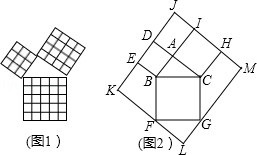 勾股定理被誉为“几何明珠”,在数学的发展历程中占有举足轻重的地位.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=3,AC=4,点D、E、F、G、H、I 都在长方形KLMJ的边上,则长方形KLMJ的面积为( )
勾股定理被誉为“几何明珠”,在数学的发展历程中占有举足轻重的地位.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=3,AC=4,点D、E、F、G、H、I 都在长方形KLMJ的边上,则长方形KLMJ的面积为( )
 勾股定理被誉为“几何明珠”,在数学的发展历程中占有举足轻重的地位.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=3,AC=4,点D、E、F、G、H、I 都在长方形KLMJ的边上,则长方形KLMJ的面积为( )
勾股定理被誉为“几何明珠”,在数学的发展历程中占有举足轻重的地位.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=3,AC=4,点D、E、F、G、H、I 都在长方形KLMJ的边上,则长方形KLMJ的面积为( )| A. | 90 | B. | 100 | C. | 110 | D. | 121 |
14. 如图,在△ABC中,DE垂直平分AC,若BC=20cm,AB=12cm,则△ABD的周长为( )
如图,在△ABC中,DE垂直平分AC,若BC=20cm,AB=12cm,则△ABD的周长为( )
 如图,在△ABC中,DE垂直平分AC,若BC=20cm,AB=12cm,则△ABD的周长为( )
如图,在△ABC中,DE垂直平分AC,若BC=20cm,AB=12cm,则△ABD的周长为( )| A. | 20cm | B. | 22cm | C. | 26cm | D. | 32cm |
13.已知a+2与2a-5都是m的平方根,则m的值是( )
| A. | 1 | B. | 9 | C. | -3 | D. | 3 |
12.如果a、b、c是一个直角三角形的三边,则a:b:c可以等于( )
| A. | 2:2:4 | B. | 3:4:5 | C. | 3:5:7 | D. | 1:3:9 |
11.等腰三角形的周长是16,一边长为4,则这个等腰三角形腰长为( )
0 311327 311335 311341 311345 311351 311353 311357 311363 311365 311371 311377 311381 311383 311387 311393 311395 311401 311405 311407 311411 311413 311417 311419 311421 311422 311423 311425 311426 311427 311429 311431 311435 311437 311441 311443 311447 311453 311455 311461 311465 311467 311471 311477 311483 311485 311491 311495 311497 311503 311507 311513 311521 366461
| A. | 4 | B. | 6 | C. | 4或6 | D. | 8 |
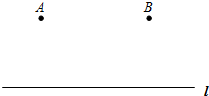 如图:A村和B村在公路l同侧,且AB=3千米,两村距离公路都是2千米.现决定在公路l上建立一个供水站P,要求使PA+PB最短.
如图:A村和B村在公路l同侧,且AB=3千米,两村距离公路都是2千米.现决定在公路l上建立一个供水站P,要求使PA+PB最短.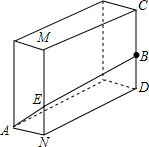 如图,一块长方体砖宽AN=5cm,长ND=10cm,CD上的点B距地面的高BD=8cm,地面上A处的一只蚂蚁到B处吃食,需要爬行的最短路径是17cm.
如图,一块长方体砖宽AN=5cm,长ND=10cm,CD上的点B距地面的高BD=8cm,地面上A处的一只蚂蚁到B处吃食,需要爬行的最短路径是17cm.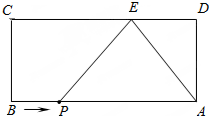 如图,已知正方形ABCD,AB=8,AD=4,E为CD边上一点,CE=5.
如图,已知正方形ABCD,AB=8,AD=4,E为CD边上一点,CE=5.