13.阅读与思考;
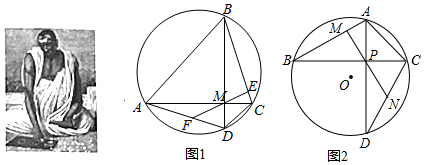
(1)请你阅读婆罗摩笈多定理的证明过程,完成婆罗摩笈多逆定理的证明:
已知:如图1,四边形ABCD内接与圆O,对角线AC⊥BD于点M,F是AD中点,连接FM并延长交BC于点E,求证:ME⊥BC
(2)已知如图2,△ABC内接于圆O,∠B=30°∠ACB=45°,AB=2,点D在圆O上,∠BCD=60°,连接AD 交BC于点P,作ON⊥CD于点N,延长NP交AB于点M,求证PM⊥BA并求PN的长.
| 婆罗摩笈多是一位印度数学家与天文学家,书写了两部关于数学与天文的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数及加减法运算仅晚于中国九章算术而他的负数乘除法法则在全世界都是领先的,他还提出了著名的婆罗摩笈多定理,该定理的内容及证明如下: 已知:如图,四边形ABCD内接与圆O对角线AC⊥BD于点M,ME⊥BC于点E,延长EM交CD于F,求证:MF=DF 证明∵AC⊥BD,ME⊥BC ∴∠CBD=∠CME ∵∠CBD=∠CAD,∠CME=∠AMF ∴∠CAD=∠AMF ∴AF=MF ∵∠AMD=90°,同时∠MAD+∠MDA=90° ∴∠FMD=∠FDM ∴MF=DF,即F是AD中点. |

(1)请你阅读婆罗摩笈多定理的证明过程,完成婆罗摩笈多逆定理的证明:
已知:如图1,四边形ABCD内接与圆O,对角线AC⊥BD于点M,F是AD中点,连接FM并延长交BC于点E,求证:ME⊥BC
(2)已知如图2,△ABC内接于圆O,∠B=30°∠ACB=45°,AB=2,点D在圆O上,∠BCD=60°,连接AD 交BC于点P,作ON⊥CD于点N,延长NP交AB于点M,求证PM⊥BA并求PN的长.
10.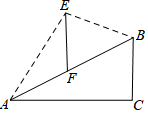 如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )
如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )
 如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )
如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )| A. | 16.9 米 | B. | 13.7米 | C. | 14.6米 | D. | 15.2米 |
8.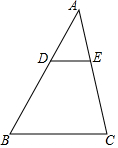 如图,D、E分别是△ABC的边AB、AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )
如图,D、E分别是△ABC的边AB、AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )
0 298381 298389 298395 298399 298405 298407 298411 298417 298419 298425 298431 298435 298437 298441 298447 298449 298455 298459 298461 298465 298467 298471 298473 298475 298476 298477 298479 298480 298481 298483 298485 298489 298491 298495 298497 298501 298507 298509 298515 298519 298521 298525 298531 298537 298539 298545 298549 298551 298557 298561 298567 298575 366461
 如图,D、E分别是△ABC的边AB、AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )
如图,D、E分别是△ABC的边AB、AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )| A. | 4 | B. | 8 | C. | $\frac{21}{2}$ | D. | $\frac{25}{2}$ |
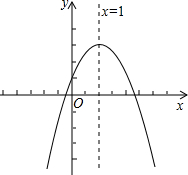 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论: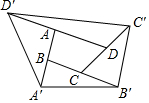 如图,把四边形ABCD的各边延长,使得AB=BA',BC=CB',CD=DC',DA=AD',得到一个大的四边形A'B'C'D',若四边形ABCD的面积是1,求四边形A'B'C'D'的面积.
如图,把四边形ABCD的各边延长,使得AB=BA',BC=CB',CD=DC',DA=AD',得到一个大的四边形A'B'C'D',若四边形ABCD的面积是1,求四边形A'B'C'D'的面积. 如图:在等腰Rt△ABC中,BD=AE,BF与DE垂直,求证:ED=BF.
如图:在等腰Rt△ABC中,BD=AE,BF与DE垂直,求证:ED=BF.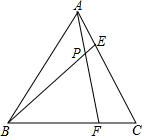 如图,在等边△ABC中,点F、E分别在BC、AC边上,AE=CF,AF与BE相交于点P.
如图,在等边△ABC中,点F、E分别在BC、AC边上,AE=CF,AF与BE相交于点P.