题目内容
14.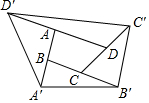 如图,把四边形ABCD的各边延长,使得AB=BA',BC=CB',CD=DC',DA=AD',得到一个大的四边形A'B'C'D',若四边形ABCD的面积是1,求四边形A'B'C'D'的面积.
如图,把四边形ABCD的各边延长,使得AB=BA',BC=CB',CD=DC',DA=AD',得到一个大的四边形A'B'C'D',若四边形ABCD的面积是1,求四边形A'B'C'D'的面积.
分析 根据“四边形ABCD的面积是1”,要求四边形A′B′C′D′的面积,只要求出多出来的四个三角形的面积即可.
解答  解:如图,连接AC,BD.
解:如图,连接AC,BD.
对△AA'D'分析,可知其底AD'=AD,其高即A'到DD'的距离为B到DD'距离的两倍,
即△AA'D'与△ABD底相等,前者高为后者的两倍,
于是△AA'D'的面积为△ABD的面积的两倍,
同理,△CB'C'的面积为△BCD面积的两倍,
于是△AA'D'与△CB'C'的面积和为四边形ABCD面积的2倍,为2,
同理△DD'C'与△BB'A'的面积和也为2,
所以多出来的四个三角形的面积和为4,
四边形A'B'C'D'的面积为:4+1=5,
故四边形A′B′C′D′的面积是5.
点评 本题考查了三角形的面积,解答此题的关键是,根据题意,添加辅助线,利用三角形的面积公式,帮助我们找到三角形之间的关系,由此即可解答.

练习册系列答案
相关题目
2.铁一课间餐种类繁多,深受学生喜爱.这天饭堂在课间的出品有鸡腿、薯饼、鱼丸和鸡柳.某同学就九年级学生对课间餐各类食物的喜爱程度做了抽样调查,制成表格如下:
(1)样本容量是250,a=12%,b=30,c=16%.
(2)若小王和小李商议着一起去买课间餐,若他们对以上四种口味的课间餐喜爱程度相同.请你帮他们算一算他们买了相同课间餐的概率.
| 课间餐种类 | 人类 | 百分比 |
| 鸡腿 | 150 | 60% |
| 薯饼 | 30 | a |
| 鱼丸 | b | 12% |
| 鸡柳 | 40 | c |
(2)若小王和小李商议着一起去买课间餐,若他们对以上四种口味的课间餐喜爱程度相同.请你帮他们算一算他们买了相同课间餐的概率.
4.甲、乙、丙三位同学分别正确指出了某一个函数的一个性质.甲:函数图象经过第一象限;乙:函数图象经过第三象限;丙:每第一个象限内,y值随x值的增大而减小.根据他们的描述,这个函数表达式可能是( )
| A. | y=2x | B. | y=$\frac{2}{x}$ | C. | y=-$\frac{1}{x}$ | D. | y=2x2 |
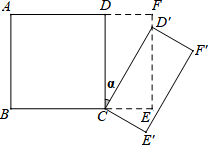 如图所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.当点D′恰好落在EF边上时,旋转角α的值为30°.
如图所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.当点D′恰好落在EF边上时,旋转角α的值为30°.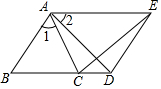 如图,已知∠1=∠2,AB=AC,AD=AE,且B、C、D三点共线.
如图,已知∠1=∠2,AB=AC,AD=AE,且B、C、D三点共线. 如图,AC=AD,BC=BD,图中有相等的角吗?若没有说明理由,若有请全部找出来,并证明其中的一组角相等.
如图,AC=AD,BC=BD,图中有相等的角吗?若没有说明理由,若有请全部找出来,并证明其中的一组角相等.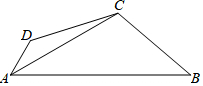 如图,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,AC=4,CD=3,则AB-AD=2$\sqrt{5}$.
如图,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,AC=4,CD=3,则AB-AD=2$\sqrt{5}$.