15．
如图，在△ABC中，D、E、F分别是边AB、AC、BC上的点，连接EF，CD相交于点G，若四边形BDEF是平行四边形，则下列说法不正确的是（ ）
如图，在△ABC中，D、E、F分别是边AB、AC、BC上的点，连接EF，CD相交于点G，若四边形BDEF是平行四边形，则下列说法不正确的是（ ）| A． | $\frac{AD}{DB}$=$\frac{DG}{CG}$ | B． | $\frac{AD}{DB}$=$\frac{EG}{GF}$ | C． | $\frac{AD}{DB}$=$\frac{BF}{BC}$ | D． | $\frac{AD}{DB}$=$\frac{DE}{FC}$ |
14．
如图所示，一艘船从A点出发，沿东北方向航行至点B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC的余角是（ ）
如图所示，一艘船从A点出发，沿东北方向航行至点B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC的余角是（ ）| A． | 15° | B． | 30° | C． | 45° | D． | 75° |
13．下列四个几何体中，俯视图为正方形的是（ ）
| A． |  球 | B． |  圆柱 | C． |  圆锥 | D． |  正方形 |
12．已知点P（a，b）在反比例函数y=-$\frac{6}{x}$的图象上，则ab的值为（ ）
| A． | 6 | B． | $\frac{1}{6}$ | C． | -6 | D． | -$\frac{1}{6}$ |
11．在数$\frac{2}{3}$，1，-3，0中，绝对值最大的数是（ ）
| A． | $\frac{2}{3}$ | B． | 1 | C． | -3 | D． | 0 |
如图所示得到几何体是由一个圆柱体和一个长方形组成的，则这个几何体的左视图是（ ）
9．
如图所示格点图中，每个小正方形的边长均为1，△ABC的三个顶点均在格点上，以原点O为位似中心，相似比为$\frac{1}{2}$，把△ABC缩小，则点C的对应点C′的坐标为（ ）
如图所示格点图中，每个小正方形的边长均为1，△ABC的三个顶点均在格点上，以原点O为位似中心，相似比为$\frac{1}{2}$，把△ABC缩小，则点C的对应点C′的坐标为（ ）| A． | （1，$\frac{3}{2}$） | B． | （2，6） | C． | （2，6）或（-2，-6） | D． | （1，$\frac{3}{2}$）或（-1，-$\frac{3}{2}$） |
8．
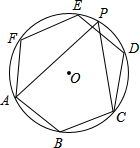如图，正六边形ABCDEF内接于⊙O，点P为$\widehat{DE}$上一点，则tan∠APC的值为（ ）
如图，正六边形ABCDEF内接于⊙O，点P为$\widehat{DE}$上一点，则tan∠APC的值为（ ）| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | 1 |
7．我们在探究“任意一个四边形内角和是多少度？”时，采用的方法是连接四边形的一条对角线，把四边形分割成两个三角形，从而探究出任意四边形的内角和等于360°，这一过程体现的数学思想是（ ）
| A． | 转化思想 | B． | 方程思想 | C． | 函数思想 | D． | 数形结合思想 |
6．（-2）×3的结果是（ ）
0 284155 284163 284169 284173 284179 284181 284185 284191 284193 284199 284205 284209 284211 284215 284221 284223 284229 284233 284235 284239 284241 284245 284247 284249 284250 284251 284253 284254 284255 284257 284259 284263 284265 284269 284271 284275 284281 284283 284289 284293 284295 284299 284305 284311 284313 284319 284323 284325 284331 284335 284341 284349 366461
| A． | 6 | B． | -6 | C． | 1 | D． | -5 |