7.我省深入推进千万亩森林增长工程,2015年新造林226.3万亩,其中226.3万用科学记数法表示为( )
| A. | 226.3×104 | B. | 2.263×105 | C. | 2.263×106 | D. | 2.263×107 |
6.现给出四个命题:①等边三角形既是轴对称图形,又是中心对称图形;②相似三角形的面积比等于它们的相似比;③菱形的面积等于两条对角线的积;④一组数据2,5,4,3,3的中位数是4,众数是3,其中不正确的命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.以下问题,不适合用普查的是( )
0 283331 283339 283345 283349 283355 283357 283361 283367 283369 283375 283381 283385 283387 283391 283397 283399 283405 283409 283411 283415 283417 283421 283423 283425 283426 283427 283429 283430 283431 283433 283435 283439 283441 283445 283447 283451 283457 283459 283465 283469 283471 283475 283481 283487 283489 283495 283499 283501 283507 283511 283517 283525 366461
| A. | 了解全班同学每周体育锻炼的时间 | |
| B. | 为了了解“嫦娥二号”卫星零部件的状况 | |
| C. | 学校招聘教师,对应聘人员面试 | |
| D. | 了解一批灯泡的使用寿命 |
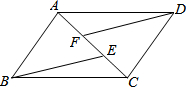 如图,在?ABCD中,点E、F在AC上,且AF=CE,求证:∠ABE=∠CDF.
如图,在?ABCD中,点E、F在AC上,且AF=CE,求证:∠ABE=∠CDF.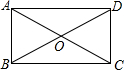 如图,矩形ABCD的对角线相交于O,要使它成为正方形,应添加的条件是AB=BC(只填写一个条件即可)
如图,矩形ABCD的对角线相交于O,要使它成为正方形,应添加的条件是AB=BC(只填写一个条件即可) 如图,点A在双曲线y=$\frac{m}{x}$上,点B在双曲线y=$\frac{n}{x}$(n>m>0)上,C、D在x轴上,若四边形ABCD为平行四边形且面积为5,则m-n等于-5.
如图,点A在双曲线y=$\frac{m}{x}$上,点B在双曲线y=$\frac{n}{x}$(n>m>0)上,C、D在x轴上,若四边形ABCD为平行四边形且面积为5,则m-n等于-5.