15.下列能构成直角三角形的一组数是( )
0 282675 282683 282689 282693 282699 282701 282705 282711 282713 282719 282725 282729 282731 282735 282741 282743 282749 282753 282755 282759 282761 282765 282767 282769 282770 282771 282773 282774 282775 282777 282779 282783 282785 282789 282791 282795 282801 282803 282809 282813 282815 282819 282825 282831 282833 282839 282843 282845 282851 282855 282861 282869 366461
| A. | 2、3、4 | B. | 6、8、9 | C. | 5、12、13 | D. | 1、1、2 |
 如图,若直线a∥b,那么∠x=64度.
如图,若直线a∥b,那么∠x=64度.

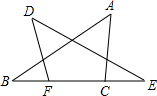 如图,点F、C在BE上,BF=CE,∠A=∠D,∠B=∠E.
如图,点F、C在BE上,BF=CE,∠A=∠D,∠B=∠E.