如图，有一块直角三角形纸片ABC，∠C=90°．两直角边AC=6cm，BC=8cm，现将该纸片沿直线AD折叠，使点C落在斜边AB上的点E处，则折痕AD=3$\sqrt{5}$cm．
9．
有这样一个问题：探究函数y=$\frac{1}{{{x^2}-1}}$的图象与性质．
小东根据学习函数的经验，对函数y=$\frac{1}{{{x^2}-1}}$的图象与性质进行了探究．下面是小东的探究过程，请补充完成：
（1）自变量取值范围：x≠±1
（2）画图象
①列表
②描点：（见坐标系）
③连线：请你在坐标系中补全图象
（3）进一步探究发现，该函数图象在y轴上有一交点为（0，-1），结合图象，请你写出该函数的其他性质
（一条即可）：x＜-1时y随x增大而增大．
有这样一个问题：探究函数y=$\frac{1}{{{x^2}-1}}$的图象与性质．小东根据学习函数的经验，对函数y=$\frac{1}{{{x^2}-1}}$的图象与性质进行了探究．下面是小东的探究过程，请补充完成：
（1）自变量取值范围：x≠±1
（2）画图象
①列表
| x | … | -$\frac{9}{4}$ | -2 | -$\frac{7}{4}$ | -$\frac{3}{2}$ | -$\frac{5}{4}$ | … |
| y | … | 0.25 | 0.33 | 0.48 | 0.8 | 1.78 | … |
| x | -$\frac{3}{4}$ | -$\frac{1}{2}$ | $\frac{1}{4}$ | 0 | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{3}{4}$ |
| y | -2.29 | -1.33 | -1.07 | -1 | -1.07 | -1.33 | -2.29 |
| x | … | $\frac{5}{4}$ | $\frac{3}{2}$ | $\frac{7}{4}$ | 2 | $\frac{9}{4}$ | … |
| y | … | 1.78 | 0.8 | 0.48 | 0.33 | 0.25 | … |
③连线：请你在坐标系中补全图象
（3）进一步探究发现，该函数图象在y轴上有一交点为（0，-1），结合图象，请你写出该函数的其他性质
（一条即可）：x＜-1时y随x增大而增大．
8．
如图，△ABC中，AB⊥BC，BE⊥AC，∠1=∠2，AD=AB，则下列结论不正确的是（ ）
如图，△ABC中，AB⊥BC，BE⊥AC，∠1=∠2，AD=AB，则下列结论不正确的是（ ）| A． | BF=DF | B． | ∠1=∠EFD | C． | BF＞EF | D． | FD∥BC |
7．
小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．
如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（ ）
小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（ ）
| A． | 角的内部到角的两边的距离相等的点在角的平分线上 | |
| B． | 角平分线上的点到这个角两边的距离相等 | |
| C． | 三角形三条角平分线的交点到三条边的距离相等 | |
| D． | 以上均不正确 |
6．
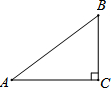已知，如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，则sinB的值是（ ）
已知，如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，则sinB的值是（ ）| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
5．
如图，已知∠A=n°，若P1点是∠ABC和外角∠ACE的角平分线的交点，P2点是∠P1BC和外角∠P1CE的角平分线的交点，P3点是∠P2BC和外角∠P2CE的交点…依此类推，则∠Pn=（ ）
如图，已知∠A=n°，若P1点是∠ABC和外角∠ACE的角平分线的交点，P2点是∠P1BC和外角∠P1CE的角平分线的交点，P3点是∠P2BC和外角∠P2CE的交点…依此类推，则∠Pn=（ ）| A． | $\frac{n°}{2n}$ | B． | $\frac{n°}{2^n}$ | C． | $\frac{n°}{{{2^{n-1}}}}$ | D． | $\frac{n°}{2（n-1）}$ |
4．如图在表中填在各正方形中的四个数之间都有相同的规律，根据此规律，m的值是（ ）
0 279718 279726 279732 279736 279742 279744 279748 279754 279756 279762 279768 279772 279774 279778 279784 279786 279792 279796 279798 279802 279804 279808 279810 279812 279813 279814 279816 279817 279818 279820 279822 279826 279828 279832 279834 279838 279844 279846 279852 279856 279858 279862 279868 279874 279876 279882 279886 279888 279894 279898 279904 279912 366461
| A． | 74 | B． | 104 | C． | 126 | D． | 144 |
已知，如图，在△AFD和△CEB中，点A，E，F，C在同一直线上，AE=CF，DF=BE，AD=CB．求证：AD∥BC．