题目内容
10．
如图，有一块直角三角形纸片ABC，∠C=90°．两直角边AC=6cm，BC=8cm，现将该纸片沿直线AD折叠，使点C落在斜边AB上的点E处，则折痕AD=3$\sqrt{5}$cm．
分析 先根据勾股定理求得AB的长，再根据折叠的性质求得AE，BE的长，从而利用勾股定理可求得CD的长，然后根据勾股定理即可求得AD．
解答 解：∵AC=6cm，BC=8cm，∠C=90°
∴AB=10cm，
∵AE=6cm（折叠的性质），
∴BE=4cm，
设CD=x，
则在Rt△DEB中，
42+x2=（8-x）2，
∴x=3cm．
∴CD=3cm，
在Rt△ACD中，AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=3$\sqrt{5}$cm．
故答案为3$\sqrt{5}$．
点评 本题考查了翻折变换的性质，勾股定理的应用，熟记性质并表示出Rt△DEB的三边，然后利用勾股定理列出方程是解题的关键．
练习册系列答案
相关题目
已知：如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点M，交BC于点N，连接AN，过点C的切线交AB的延长线于点P．
操作探究：已知在纸面上有一数轴（如图所示），
5．
如图，已知∠A=n°，若P1点是∠ABC和外角∠ACE的角平分线的交点，P2点是∠P1BC和外角∠P1CE的角平分线的交点，P3点是∠P2BC和外角∠P2CE的交点…依此类推，则∠Pn=（ ）
如图，已知∠A=n°，若P1点是∠ABC和外角∠ACE的角平分线的交点，P2点是∠P1BC和外角∠P1CE的角平分线的交点，P3点是∠P2BC和外角∠P2CE的交点…依此类推，则∠Pn=（ ）| A． | $\frac{n°}{2n}$ | B． | $\frac{n°}{2^n}$ | C． | $\frac{n°}{{{2^{n-1}}}}$ | D． | $\frac{n°}{2（n-1）}$ |
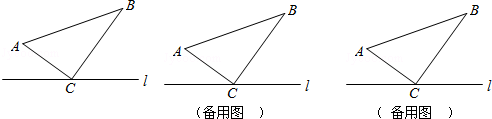
某地因持续高温干旱，村民饮水困难，镇政府组织村民组成水源行动小组到村镇周边找水．某村民在山洞C里发现了暗河（如图所示），经勘察，在山洞的西面有一条南北走向的公路连接着A，B两村庄，山洞C位于A村庄南偏东30°方向，且位于B村庄南偏东60°方向．为方便A，B两村庄的村民取水，准备从山洞C处向公路AB紧急修建一条最近的简易公路CD，现已知A，B两村庄相距6千米．