题目内容
11.△ABC中,BC=4,∠A=60°,则这个三角形的面积的最大值是4$\sqrt{3}$.分析 根据题意得到△ABC为等边三角形时,这个三角形的面积最大,求出此时三角形的面积即可.
解答  解:根据圆周角定理可知,当△ABC为等边三角形时,这个三角形的面积最大,
解:根据圆周角定理可知,当△ABC为等边三角形时,这个三角形的面积最大,
∵AD⊥BC,
∴BD=$\frac{1}{2}$BC=2,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=2$\sqrt{3}$,
∴△ABC的面积为:$\frac{1}{2}$×BC×AD=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查的是圆周角定理和垂径定理的应用,确定面积最大时三角形的形状是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列各组数中,能构成直角三角形的一组是( )
| A. | 6,8,12 | B. | 1,4,$\sqrt{3}$ | C. | 3,4,5 | D. | 2,2,$\sqrt{5}$ |
6.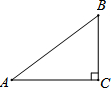 已知,如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinB的值是( )
已知,如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinB的值是( )
 已知,如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinB的值是( )
已知,如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinB的值是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
16.今年铁路大提速,小明的爸爸因要出差,于是去火车站查询列车的开行时间.下面是小明的爸爸从火车站带回家的最新时刻表:
小明的爸爸找出以前同一车次的时刻表如下:
比较了两张时刻表后,小明的爸爸提出了如下问题,请你帮小明解答:
(1)请直接写出现在该次列车的运行时间是多少小时?
(2)现在该次列车的运行时间比以前缩短了多少小时?
(3)若该次列车提速后的平均时速为每小时200千米,那么,该次列车原来的平均时速为多少?(结果精确到个位)
| 2015年10月18日起1008次列车时刻表 | |||
| 始发点 | 发车时间 | 终点站 | 到站时间 |
| A站 | 上午8:20 | B站 | 次日12:20 |
| 2014年1008次列车时刻表 | |||
| 始发点 | 发车时间 | 终点站 | 到站时间 |
| A站 | 下午14:30 | B站 | 第三日8:30 |
(1)请直接写出现在该次列车的运行时间是多少小时?
(2)现在该次列车的运行时间比以前缩短了多少小时?
(3)若该次列车提速后的平均时速为每小时200千米,那么,该次列车原来的平均时速为多少?(结果精确到个位)
 如图,一次函数y=-x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合.
如图,一次函数y=-x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合. 如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°
如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°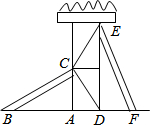 某游乐场有两个长度相同的滑梯,要想使左边滑梯BC的高度AC与右边滑梯EF的水平方向的长度DF相等,则两个滑梯的倾斜角∠ABC与∠DFE的大小必须满足什么关系?说明理由.
某游乐场有两个长度相同的滑梯,要想使左边滑梯BC的高度AC与右边滑梯EF的水平方向的长度DF相等,则两个滑梯的倾斜角∠ABC与∠DFE的大小必须满足什么关系?说明理由.