10.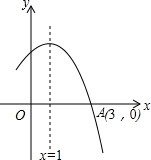 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(3,0),二次函数图象对称轴为直线x=1,给出五个结论:①bc>0;②a+b+c<0;③当x<1时,y随x的增大而增大;④方程ax2+bx+c=0的根为x1=-1,x2=3;⑤4a-2b+c>0其中正确结论是( )
如图所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(3,0),二次函数图象对称轴为直线x=1,给出五个结论:①bc>0;②a+b+c<0;③当x<1时,y随x的增大而增大;④方程ax2+bx+c=0的根为x1=-1,x2=3;⑤4a-2b+c>0其中正确结论是( )
 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(3,0),二次函数图象对称轴为直线x=1,给出五个结论:①bc>0;②a+b+c<0;③当x<1时,y随x的增大而增大;④方程ax2+bx+c=0的根为x1=-1,x2=3;⑤4a-2b+c>0其中正确结论是( )
如图所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(3,0),二次函数图象对称轴为直线x=1,给出五个结论:①bc>0;②a+b+c<0;③当x<1时,y随x的增大而增大;④方程ax2+bx+c=0的根为x1=-1,x2=3;⑤4a-2b+c>0其中正确结论是( )| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ③④⑤ |
9.已知函数y=2(x-3)2-4(1≤x≤6)的最大值与最小值的和为( )
0 278995 279003 279009 279013 279019 279021 279025 279031 279033 279039 279045 279049 279051 279055 279061 279063 279069 279073 279075 279079 279081 279085 279087 279089 279090 279091 279093 279094 279095 279097 279099 279103 279105 279109 279111 279115 279121 279123 279129 279133 279135 279139 279145 279151 279153 279159 279163 279165 279171 279175 279181 279189 366461
| A. | 18 | B. | 0 | C. | 10 | D. | 无法确定 |
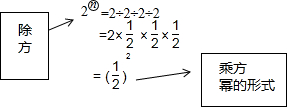 概念学习
概念学习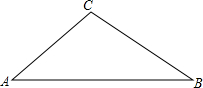 如图,在△ABC中,∠A=45°,tanB=$\frac{3}{4}$,BC=10,则AB的长为14.
如图,在△ABC中,∠A=45°,tanB=$\frac{3}{4}$,BC=10,则AB的长为14.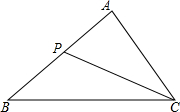 如图,已知△ACP∽△ABC,AC=6,AP=3,则AB的长为12.
如图,已知△ACP∽△ABC,AC=6,AP=3,则AB的长为12.