3. 我们曾经通过列表、画图象,研究了函数y=ax2(a≠0)的性质,知道它的图象是一条抛物线,通过图象还研究了它的相关性质;经过平移函数y=ax2(a≠0)的图象还可得到函数y=a(x-h)2+k,(a≠0)的图象.用类似的方法还可研究其他函数的有关性质.
我们曾经通过列表、画图象,研究了函数y=ax2(a≠0)的性质,知道它的图象是一条抛物线,通过图象还研究了它的相关性质;经过平移函数y=ax2(a≠0)的图象还可得到函数y=a(x-h)2+k,(a≠0)的图象.用类似的方法还可研究其他函数的有关性质.
下面请你通过类比,尝试研究一下函数y=$\frac{1}{2}$x3的性质:
(1)完成下表:
(2)在所给坐标系中作出函数y=$\frac{1}{2}$x3的图象;
(3)观察你画的函数y=$\frac{1}{2}$x3的图象,回答下列问题:
①函数y=$\frac{1}{2}$x3图象的对称性下列说法正确的是C.
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.既不是轴对称也不是中心对称
②随x的增大,y有怎样的变化?
③y是否有最大或最小值?
④将函数y=$\frac{1}{2}$x3的图象向左平移一个单位,再向上平移两个单位.可得到怎样的函数表达式,请直接将你的猜想写出来?
0 278745 278753 278759 278763 278769 278771 278775 278781 278783 278789 278795 278799 278801 278805 278811 278813 278819 278823 278825 278829 278831 278835 278837 278839 278840 278841 278843 278844 278845 278847 278849 278853 278855 278859 278861 278865 278871 278873 278879 278883 278885 278889 278895 278901 278903 278909 278913 278915 278921 278925 278931 278939 366461
 我们曾经通过列表、画图象,研究了函数y=ax2(a≠0)的性质,知道它的图象是一条抛物线,通过图象还研究了它的相关性质;经过平移函数y=ax2(a≠0)的图象还可得到函数y=a(x-h)2+k,(a≠0)的图象.用类似的方法还可研究其他函数的有关性质.
我们曾经通过列表、画图象,研究了函数y=ax2(a≠0)的性质,知道它的图象是一条抛物线,通过图象还研究了它的相关性质;经过平移函数y=ax2(a≠0)的图象还可得到函数y=a(x-h)2+k,(a≠0)的图象.用类似的方法还可研究其他函数的有关性质.下面请你通过类比,尝试研究一下函数y=$\frac{1}{2}$x3的性质:
(1)完成下表:
| x | … | -2 | -1 | 0 | 1 | 2 | … | ||
| y | … | 0 | 4 | … |
(3)观察你画的函数y=$\frac{1}{2}$x3的图象,回答下列问题:
①函数y=$\frac{1}{2}$x3图象的对称性下列说法正确的是C.
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.既不是轴对称也不是中心对称
②随x的增大,y有怎样的变化?
③y是否有最大或最小值?
④将函数y=$\frac{1}{2}$x3的图象向左平移一个单位,再向上平移两个单位.可得到怎样的函数表达式,请直接将你的猜想写出来?
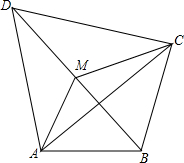 如图,已知四边形ABCD,M是BD的中点.
如图,已知四边形ABCD,M是BD的中点.
 如图,已知ABCD为正方形,∠FED=∠BEC,EF=CE,求证:DF+EF=BE.
如图,已知ABCD为正方形,∠FED=∠BEC,EF=CE,求证:DF+EF=BE. 已知二次函数图象的顶点在原点O,对称轴为y轴.一次函数y=kx+1的图象与二次函数的图象交于A、B两点(A在B的左侧),且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.
已知二次函数图象的顶点在原点O,对称轴为y轴.一次函数y=kx+1的图象与二次函数的图象交于A、B两点(A在B的左侧),且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.
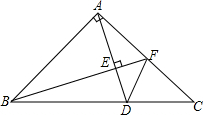 已知△ABC,AB=AC,∠BAC=90°,点F在AC的中点,AD⊥BF,垂足为E,若DE=2,则△ADF的面积为$\frac{15}{4}$.
已知△ABC,AB=AC,∠BAC=90°,点F在AC的中点,AD⊥BF,垂足为E,若DE=2,则△ADF的面积为$\frac{15}{4}$.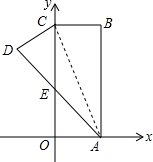 如图,在直角坐标系中,长方形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(2,6),将长方形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E,则点D的坐标为(-$\frac{8}{5}$,$\frac{24}{5}$).
如图,在直角坐标系中,长方形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(2,6),将长方形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E,则点D的坐标为(-$\frac{8}{5}$,$\frac{24}{5}$).