题目内容
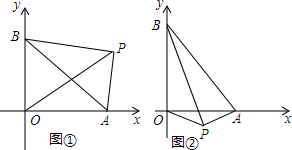
6.如图:已知A(a,0)、B(0,b),且a、b满足(a-2)2+|2b-4|=0.(1)如图1,求△AOB的面积;
(2)如图2,点C在线段AB上(不与A、B重合)移动,AB⊥BD,且∠COD=45°,猜想线段AC、BD、CD之间的数量关系并证明你的结论;
(3)如图3,若P为x轴上异于原点O和点A的一个动点,连接PB,将线段PB绕点P顺时针旋转90°至PE,直线AE交y轴Q,点Q,当P点在x轴上移动时,线段BE和线段BQ中,请判断哪条线段长为定值,并求出该定值.
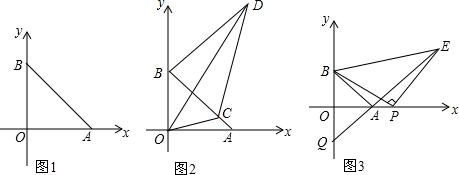
分析 (1)根据非负数的性质得到a-2=0,2b-4=0,求得a=2,b=2,得到OA=2,OB=2,于是得到结果;
(2)证明:将△AOC绕点O逆时针旋转90°得到△OBF根据已知条件得到∠BDF=180°,由∠DOC=45°,∠AOB=90°,同时代的∠BOD+∠AOC=45°,求出∠FOD=∠BOF+∠BOD=∠BOD+∠AOC=45°,推出△ODF≌△ODC,根据全等三角形的性质得到DC=DF=DB+BF=DB+DC;
(3)BQ是定值,作EF⊥OA于F,在FE上截取PF=FD,由∠BAO=∠PDF=45°,得到∠PAB=∠PD,E=135°,根据余角的性质得到∠BPA=∠PED,推出△PBA≌EPD,根据全等三角形的性质得到AP=ED,于是得到FD+ED=PF+AP.即:FE=FA,根据等腰直角三角形的性质得到结论.
解答 (1)解:∵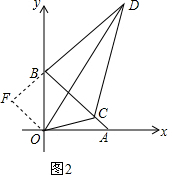 (a-2)2+|2b-4|=0,∴a-2=0,2b-4=0,
(a-2)2+|2b-4|=0,∴a-2=0,2b-4=0,
∴a=2,b=2,
∴A(2,0)、B(0,2),
∴OA=2,OB=2,
∴△AOB的面积=$\frac{1}{2}×2×2$=2;
(2)证明:将△AOC绕点O逆时针旋转90°得到△OBF,
∵∠OAC=∠OBF=∠OBA=45°,∠DBA=90°,
∴∠BDF=180°,
∵∠DOC=45°,∠AOB=90°,
∴∠BOD+∠AOC=45°,
∴∠FOD=∠BOF+∠BOD=∠BOD+∠AOC=45°,
在△ODF与△ODC中,$\left\{\begin{array}{l}{OF=OC}\\{∠FOD=∠COD}\\{OD=OD}\end{array}\right.$,
∴:△ODF≌△ODC,∴DC=DF,DF=BD+BF,故CD=BD+AC.
(3)BQ是定值,作EF⊥OA于F,在FE上截取PF=FD,
∵∠BAO=∠PDF=45°,
∴∠PAB=∠PD,E=135°,
∴∠BPA+∠EPF=90°∠EPF+∠PED=90°,
∴∠BPA=∠PED,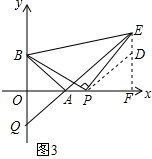
在△PBA与△EPD中,$\left\{\begin{array}{l}{PF=PD}\\{∠BPA=∠PED}\\{PB=PE}\end{array}\right.$,
∴△PBA≌EPD,
∴AP=ED,
∴FD+ED=PF+AP,
即:FE=FA,
∴∠FEA=∠FAE=45°,
∴∠QAO=∠EAF=∠OQA=45°,
∴OA=OQ=2,
∴BQ=4.
点评 本题考查了全等三角形的判定和性质,坐标与图形的性质,三角形面积的计算,正确的作出辅助线是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 5,12,13 | B. | 4,6,8 | C. | 7,24,25 | D. | 8,15,17 |
 甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地,乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,下列说法:
甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地,乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,下列说法: 如图,在△ABC中,若AB=AC,D为BC边上一点,E为AC边上的一点,且有AE=AD,∠BAD=30°,则∠CDE=15°.
如图,在△ABC中,若AB=AC,D为BC边上一点,E为AC边上的一点,且有AE=AD,∠BAD=30°,则∠CDE=15°.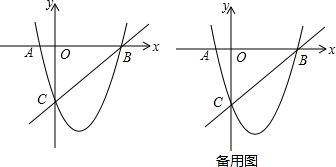
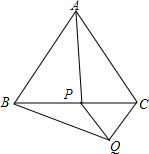 (1)如图,在等边△ABC中,在BC边上任取一点P,过点P作AC的平行线,过点C作AB的平行线,两线交于点Q.求证:AP=BQ.
(1)如图,在等边△ABC中,在BC边上任取一点P,过点P作AC的平行线,过点C作AB的平行线,两线交于点Q.求证:AP=BQ.