Question

1．如图，在平面直角坐标系中，二次函数y=ax²+bx+c的图象与x轴交于A、B两点，与y轴交于点c（0，-3），图象经过（1，-4），（-2，5），点P是抛物线在第四象限上的一动点．
（1）求二次函数解析式；
（2）是否存在点P使得点P关于直线BC的对称点在y轴上？如果存在，求点P坐标，如果不存在请说明理由；
（3）当点P运动到什么位置时，△BCP的面积最大？求出此时P点的坐标和△BCP的最大面积．

Answer 1

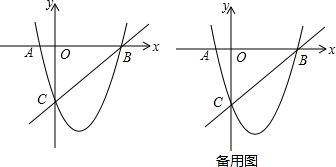
分析 （1）直接利用待定系数法求出二次函数解析式即可；
（2）首先求出二次函数与坐标轴交点，进而利用点P关于直线BC的对称点在y轴上，得出y=-3，则x²-2x-3=-3，求出P点即可；
（3）首先得出PE=PD-DE=-n²+2n+3-（3-n）=-n²+3n，再利用S_△PBC=S_△PCE+S_△PBE得出函数关系式，进而求出答案．

解答 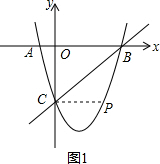解：（1）将（0，-3），（1，-4），（-2，5）代入y=ax²+bx+c得：
$\left\{\begin{array}{l}{c=-3}\\{a+b+c=-4}\\{4a-2b+c=5}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$，
故二次函数解析式为：y=x²-2x-3；

（2）存在，
理由：如图1，令y=0，则0=x²-2x-3，
解得：x₁=3，x₂=-1，
故B（3，0），
令x=0，则y=-3，
故C（0，-3），
则OB=OC，
∴∠BCO=∠OBC=45°，
∵P关于直线BC的对称点总在y轴上，
∴∠PCB=∠BCO=45°，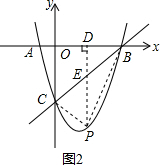
令y=-3，则x²-2x-3=-3，
解得：x₃=0，x₄=2，
故P（2，-3）；

（3）如图2，作PD⊥x轴于点D，交BC于点E，设P（n，n²-2n-3），
则PD=-n²+2n+3，
OD=n，BD=3-n，
∵∠ABC=45°，
∴DE=BD=3-n，
∵∠ABC=45°，
∴DE=BD=3-n，
∴PE=PD-DE=-n²+2n+3-（3-n）=-n²+3n，
∴S_△PBC=S_△PCE+S_△PBE
=$\frac{1}{2}$PE•OD+$\frac{1}{2}$PE•BD
=$\frac{1}{2}$PE•OB
=$\frac{1}{2}$×（-n²+3n）×3
=-$\frac{3}{2}$（n-$\frac{3}{2}$）²+$\frac{27}{8}$，
故当n=$\frac{3}{2}$时，P（$\frac{3}{2}$，-$\frac{15}{4}$），△BCP的面积最大为：$\frac{27}{8}$．

点评 此题主要考查了二次函数综合以及二次函数最值求法以及三角形面积求法和待定系数法求二次函数解析式等知识，利用数形结合表示出线段PE的长是解题关键．