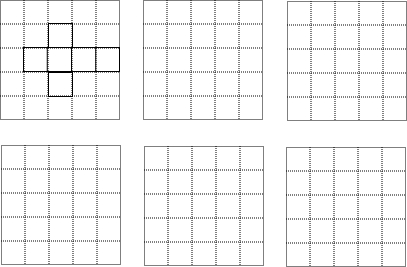
12.某市规定如下用水收费标准:每户每月用水不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按b元收费.该市某户今年3、4月份的用水量和水费如下表所示:
(1)求出a与b的值;
(2)求当用户用水为x立方米时的水费(用含x的代数式表示);
(3)某用户某月交水费39元,这个月该用户用水多少立方米?
| 月份 | 用水量(立方米) | 水费(元) |
| 3 | 5 | 7.5 |
| 4 | 9 | 27 |
(2)求当用户用水为x立方米时的水费(用含x的代数式表示);
(3)某用户某月交水费39元,这个月该用户用水多少立方米?
11.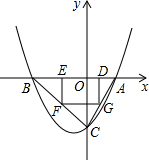 如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
(1)求抛物线表达式及A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并求出面积的最大值及m的取值范围.
 如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:| x | … | -3 | -2 | 1 | 2 | … |
| y | … | $-\frac{5}{2}$ | -4 | $-\frac{5}{2}$ | 0 | … |
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并求出面积的最大值及m的取值范围.
8.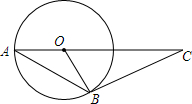 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )
 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )| A. | 65° | B. | 50° | C. | 40° | D. | 25° |
7.某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:km)
(1)求收工时距A地多远?
(2)当维修小组返回到A地时,若每km耗油0.3升,问共耗油多少升?
0 278630 278638 278644 278648 278654 278656 278660 278666 278668 278674 278680 278684 278686 278690 278696 278698 278704 278708 278710 278714 278716 278720 278722 278724 278725 278726 278728 278729 278730 278732 278734 278738 278740 278744 278746 278750 278756 278758 278764 278768 278770 278774 278780 278786 278788 278794 278798 278800 278806 278810 278816 278824 366461
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -4 | +7 | -9 | +8 | +6 | -5 | -2 |
(2)当维修小组返回到A地时,若每km耗油0.3升,问共耗油多少升?
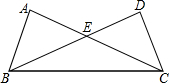 如图,在Rt△ABC和Rt△BCD中,∠A=∠D=90°,AB=CD=4,BC=$4\sqrt{5}$,△BCE的面积=10.
如图,在Rt△ABC和Rt△BCD中,∠A=∠D=90°,AB=CD=4,BC=$4\sqrt{5}$,△BCE的面积=10.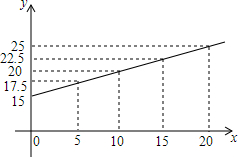 如图是弹簧挂上重物后,弹簧的长度y(厘米)与所挂物体的质量x(千克)之间的变化关系图.根据图象,回答问题:
如图是弹簧挂上重物后,弹簧的长度y(厘米)与所挂物体的质量x(千克)之间的变化关系图.根据图象,回答问题: