题目内容
4.在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段的中点坐标为$(\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2})$.(1)如图(1),C为线段AB中点,A点坐标为(0,4),B点坐标为(5,4),则点C的坐标为(2.5,4)
(2)如图(2),F为线段DE中点,D点坐标为(-4,-3),E点坐标为(1,-3).则点F的坐标为(-1.5,-3)

应用:
(1)如图(3),矩形ONDF的对角线相交于点M,ON,OF分别在x轴和y轴上,O为坐标原点,点D的坐标为(4,3),则点M的坐标为(2,1.5);
(2)在直角坐标系中.有A(-1,2),B(3,1),C(1,4)三点,另有一点D与A,B,C构成平行四边形的顶点,求D的坐标.
分析 (1)根据线段的中点公式列式计算即可得解;
(2)根据线段的中点公式列式计算即可得解;
(3)根据线段的中点公式列式计算即可得解;
(4)根据平行四边形的对角线互相平分,再运用中点公式进行求解即可.
解答 解:(1)因为C为线段AB中点,A点坐标为(0,4),B点坐标为(5,4),则点C的坐标为($\frac{0+5}{2}$,$\frac{4+4}{2}$),化简得C(2.5,4)
故答案为:(2.5,4)
(2)因为F为线段DE中点,D点坐标为(-4,-3),E点坐标为(1,-3).则点F的坐标为($\frac{-4+1}{2}$,$\frac{-3-3}{2}$),化简得F(-1.5,-3);
故答案为:(-1.5,-3).
应用(1)因为矩形ONDF的对角线互相平分且相交于点M,所以点M是OD的中点,O为坐标原点,点D的坐标为(4,3),则点M的坐标为(2,1.5);
故答案为:(2,1.5).
(2)因为A(-1,2),B(3,1),C(1,4)三点,另有一点D与A,B,C构成平行四边形的顶点,
设D的坐标为(x,y)
如图:
若AC∥BD,AB∥CD,连接对角线AD和BC,交点为E,由平行四边形对角线互相平分知,E是BC的中点,所以M($\frac{3+1}{2}$,$\frac{1+4}{2}$),M(2,2.5)
又因为M是AD的中点,所以:$\frac{-1+x}{2}=2$,$\frac{2+y}{2}=2.5$,解得x=5,y=3,所以点D(5,3)
同理可求当AD∥BC,AB∥CD时,点D(-3,5)
当AC∥BD,AD∥BC时,点D(1,-1)
综上所述:点D的坐标为:(5,3),(-3,5),(1,-1).
点评 本题考查了坐标与图形性质,主要利用了线段中点公式,理解运用公式是解题的关键.第4个问题,运用对角线互相平分得到的中点,合理运用中点公式进行运算是解题关键,注意分类讨论,不要漏解.

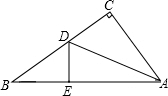 如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,AD平分∠CAB,DE⊥AB于点E,则CD=3cm.
如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,AD平分∠CAB,DE⊥AB于点E,则CD=3cm. 如图所示,甲乙两人沿着边长为60cm的正方形,按A→B→C→D→A…的方向行走,甲从A点以60m/min的速度,乙从B点以69m/min的速度行走,两人同时出发,当乙第一次追上甲时,用了20min.
如图所示,甲乙两人沿着边长为60cm的正方形,按A→B→C→D→A…的方向行走,甲从A点以60m/min的速度,乙从B点以69m/min的速度行走,两人同时出发,当乙第一次追上甲时,用了20min. 二次函数y=x2-2x-3的图象如图所示,当y>0时,自变量x的取值范围是x<-1或x>3.
二次函数y=x2-2x-3的图象如图所示,当y>0时,自变量x的取值范围是x<-1或x>3.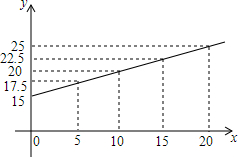 如图是弹簧挂上重物后,弹簧的长度y(厘米)与所挂物体的质量x(千克)之间的变化关系图.根据图象,回答问题:
如图是弹簧挂上重物后,弹簧的长度y(厘米)与所挂物体的质量x(千克)之间的变化关系图.根据图象,回答问题: 如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径.
如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径. 甲乙两人沿东西向公路AB同向行走,他们到点A的距离s与时间t的函数图象如图所示,请根据图象解答下列问题:
甲乙两人沿东西向公路AB同向行走,他们到点A的距离s与时间t的函数图象如图所示,请根据图象解答下列问题: