已知关于x的一元二次方程 .
.
(1)若 是此方程的一个根,求m的值;
是此方程的一个根,求m的值;
(2)试说明无论m取什么实数时,此方程总有实数根.
【答案】(1)m=-1;(2)无论m为何实数,原方程总有两个实数根
【解析】
试题分析:(1)把x=1代入方程求出m的值;
(2)根据一元二次方程根的判别式 ,由
,由 >0,有两个不相等的实数根,
>0,有两个不相等的实数根, =0,有两个相等的实数根,
=0,有两个相等的实数根, <0,没有实数根,因此由已知得
<0,没有实数根,因此由已知得 >0,求解即可.
>0,求解即可.
试题解析:【解析】
(1)把 代入方程
代入方程 得:
得:

∴
(2)∵

又∵ ≥0
≥0
即
∴无论m为何实数,原方程总有两个实数根
考点:一元二次方程的根的判别式
【题型】解答题
【适用】一般
【标题】2016届江苏省滨海县一中九年级上学期期中考试数学试卷(带解析)
【关键字标签】
【结束】
一分钟投篮测试规定:满分为10分,成绩达到6分及以上为合格,成绩达到8分及以上为优秀.甲、乙两组各15名学生的某次测试成绩如下:
成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲组(人) | 0 | 0 | 0 | 2 | 6 | 3 | 0 | 2 | 2 | 0 |
乙组(人) | 0 | 0 | 0 | 2 | 2 | 8 | 1 | 1 | 1 | 0 |
(1)请补充完成下面的成绩分析表:
统计量 | 平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 |
甲组 |
| 5 | 46.7% | |||
乙组 | 6 |
| 6 | 73.3% | 13.3% |
(2)你认为甲、乙两组哪一组的投篮成绩较好?请写出支持你的观点的理由.
一分钟投篮测试规定:满分为10分,成绩达到6分及以上为合格,成绩达到8分及以上为优秀.甲、乙两组各15名学生的某次测试成绩如下:
成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲组(人) | 0 | 0 | 0 | 2 | 6 | 3 | 0 | 2 | 2 | 0 |
乙组(人) | 0 | 0 | 0 | 2 | 2 | 8 | 1 | 1 | 1 | 0 |
(1)请补充完成下面的成绩分析表:
统计量 | 平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 |
甲组 |
| 5 | 46.7% | |||
乙组 | 6 |
| 6 | 73.3% | 13.3% |
(2)你认为甲、乙两组哪一组的投篮成绩较好?请写出支持你的观点的理由.
【答案】(1)
统计量 | 平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 |
甲组 | 6 |
| 5 | 5 | 46.7% | 26.7% |
乙组 | 6 |
| 6 | 6 | 73.3% | 13.3% |
(2)见解析
【解析】
试题分析:(1)根据平均数和中位数的定义和表中提供的数据列出算式,即可求出答案;
(2)根据甲乙两组平均数一样,乙组的方差低于甲组,再根据方差的意义和优秀率即可求出答案.
试题解析:【解析】
(1)
统计量 | 平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 |
甲组 | 6 |
| 5 | 5 | 46.7% | 26.7% |
乙组 | 6 |
| 6 | 6 | 73.3% | 13.3% |
(2)答案不唯一 认为甲组的投篮成绩较好.
理由:甲组成绩的优秀率比乙组的高.
认为乙组的投篮成绩较好.
理由:①乙组成绩的中位数比甲组的高;②乙组成绩的方差比甲组的小,乙组的成绩更稳定;③乙组成绩的合格率比甲组的高.
(只要说得有理都给分)
考点:数据分析
【题型】解答题
【适用】一般
【标题】2016届江苏省滨海县一中九年级上学期期中考试数学试卷(带解析)
【关键字标签】
【结束】
滨海县为创建“文明卫生城市”,积极投入资金进行城市道路建设与园林绿化两项工程,已知2012年投资1000万元,预计2014年投资1210万元.若这两年内平均每年投资增长的百分率相同.
(1)求平均每年投资增长的百分率;
(2)按此增长率,计算2015年投资额能否达到1360万元?
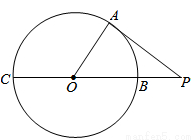
如图,AC是⊙O的直径,点B、D在⊙O上,点E在⊙O外,∠EAB=∠D=30°.

(1)∠C的度数为 °;
(2)判断直线AE与⊙O的位置关系,并说明理由;
(3)当AB=2时,求图中阴影部分的面积(结果保留根号和π).
【答案】(1)30(2)AE与⊙O相切(3)
【解析】
试题分析:(1)由圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得∠C的度数;
(2)由AB是⊙O的直径,根据半圆(或直径)所对的圆周角是直角,即可得∠ABC=90°,又由∠BCA=30°,易求得∠CAE=90°,则可得AE是⊙O的切线;
(3)过点作OH⊥AB,易得△AOB是等边三角形,然后用扇形的面积减去三角形的面积求得结果.
试题解析:【解析】
(1)30
(2)AE与⊙O相切
∵AC为⊙O的直径
∴∠ABC=90°
∵∠C=30°
∴∠BAC=60°
又∵∠EAB=30°
∴∠CAE=∠BAC +∠EAB
=90°
即AC⊥AE
又∵点A 在⊙O上
∴AE与⊙O相切
(3)过点作OH⊥AB
∵ ∠BAC=60°,OA=OB
∴△AOB为等边三角形
∴OA=AB=2
∴ AH=1,OH=
∴
∴



考点:圆周角定理,切线的判定,阴影部分的面积
【题型】解答题
【适用】一般
【标题】2016届江苏省滨海县一中九年级上学期期中考试数学试卷(带解析)
【关键字标签】
【结束】
已知某商品的进价为每件30元,九(1)班数学兴趣小组经过市场调查,整理出该商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
第x天 | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
(1)分别求出第25天和第60天商家在销售该商品时所获得的利润;
(2)问销售该商品第几天时,当天的销售利润为6050元?

 ,然后根据等弧所对的圆周角等于圆心角的一半,可求得∠BOD=40°.
,然后根据等弧所对的圆周角等于圆心角的一半,可求得∠BOD=40°.
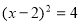 ;
; 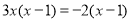
 ;
; 
 ,
, ;(2)
;(2)




 的两个实数根分别为
的两个实数根分别为 、
、 .
. ,求m的值.
,求m的值. 的两个实数根分别为
的两个实数根分别为 、
、 .
. ,求m的值.
,求m的值. ;(2)
;(2)
 =
= =0,可解得m的值;
=0,可解得m的值; ,
, ,然后代入
,然后代入




 ;(2)
;(2) ;
;
 .
.  .
. 是此方程的一个根,求m的值;
是此方程的一个根,求m的值;



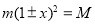 ,求得增长的百分率;
,求得增长的百分率;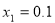 ,
,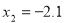 (不合题意舍去).
(不合题意舍去). 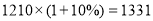 <1360
<1360 